A river or lake that flood over its borders and cause a large area of standing water may be simulated with the HYPE floodplain functionality. Read more about how the floodplains work in the model description section Floodplains.

A HYPE floodplain can only be formed from water that flows from a main river or an outlet lake; local streams and internal lakes cannot have an associated floodplain area. The floodplain and its water body are considered as one unique slc-class, and this class' area is the maximum extent of the floodplain. This means that floodplains do not constitute a new slc class and therefore the (previous) class area, that is the water body area (of main river or outlet lake), becomes larger to include the possibility to be flooded.

The modelled floodplains are described mainly by information given in the FloodData.txt file and by some parameters in the par.txt file. To use the floodplain model its model option is set in info.txt. The information in FloodData.txt can be grouped in three categories:

1. area related data; area fractions between floodplain, water bodies and subbasins (including fpfol, fpfmr)
2. elevation thresholds; thresholds between water body and flood plain and between water body and downstream lake/river (floll, flolp, flmmr, flmrp, fymol, fymmr)
3. recession coefficients; coefficients to regulate the flow between water body and floodplain (rclfp, rclpl, rclfp, rclpr).

These input data can be estimated in different ways. The suggestion here is to define those that can be observed/derived relatively easy from data (area and elevation threshold) and manually calibrate the others (recession coefficients). A method to do that is described below:

Area related data

• Determine how large area of the subbasin that can be flooded (e.g. from floodplain delineation databases, literature, etc.). Then specify how much of the floodplain area is flooded by water coming from the outlet lake (olake) and/or main river (e.g. 20% from olake and 80% from river). See example in Figure 1 where the values fpfmr and fpfol are defined this way.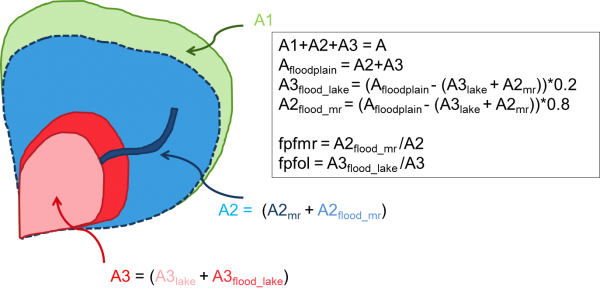

Figure 1: Example of determining fraction of floodplain area (fpfmr and fpfol). A represents the whole subbasin area, the subscripts lake and mr, outlet lake and main river, respectively.

• Introduce the area changes in GeoData.txt. A new distribution of the slc-classes' area fractions is needed, reducing the non-water classes area in favor of the water areas. Remember that the new olake area (A3 in the example in Fig 1) is composed of the original outlet lake area () plus the area flooded by the olake (); same for the new main river area. The area of the subbasin that is not flooded can be distributed between the non-water classes present in the subbasin before the changes using the same distribution as before or it can be distributed among a subset of these classes. Remember that the sum of all classes' area fractions in a subbasin needs to be one.

Elevation thresholds

• The elevation thresholds values are determined using elevation data (e.g. DEM from SRTM). The ones whose names include “ol” are related to olakes and the ones with “mr” are related to main river. Fig. 2 summarizes a way to calculate these parameters; A (flmrr and floll), B (flmrp and flolp) and C (fymol and fymmr). A is the threshold for flow from water body to floodplain. B is the threshold for flow from floodplain to water body. C is the highest elevation of the floodplain, i.e. the water level when the flood reaches its maximum areal extent.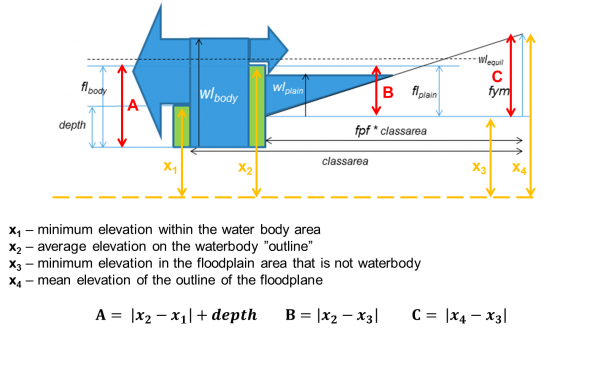

Figure 2: Illustration and definition of elevation (xi) and floodplain input (A,B,C) variables. Suggestion for determination method of elevation variables.

• All the xi are absolute distances referring to the sea level. A, B, and C are relative distances calculated based on the previous absolute values and the depth of the lake or main river (depth). The depths should be the same as HYPE uses, i.e.
  • for outlet lake: lake depth are found in LakeData.txt, DamData.txt, GeoData.txt or par.txt
  • for main river: depth is calculated from the volume and area of the main river by the equations:
  • 
  • 
  • where deadm is a general parameter (par.txt). This parameter needs to be larger than 0, when floodplains are simulated. We took it from E-HYPE and it has a value of 0.005 m2 km-2
  • To fulfil the assumptions made by HYPE of the functioning of the floodplain, the following conditions must hold: 1) A≥0, 2) B≥0 3) C≥0. If x2<x3 you can set x3=x2 to fulfill condition 2). If x4<x3 you can set x4=x3+0.1 to fulfill condition 3) with a marginal.

• If no elevation information is available, both the threshold for flow from water body to floodplain (flmrr and floll) and the threshold for flow from floodplain to water body (flmrp and flolp) can be set to zero as a starting value.

• For modeloption floodmodel 3, two extra input data are needed (hrefr and hrefl). These are the floodplain threshold in an absolute reference system. For these the value x2 can be used.

Recession coefficients

• The water levels of the river/lake and floodplain will try to reach equilibrium. The speed of equalization is determined by recession coefficients that say how far to equilibrium the water level will reach on one time step. There are separate recession coefficients for flow to and from the floodplain and for main river and outlet lake, in total four parameters (rcrfp, rcfpr, rclfp, rcfpl). The recession coefficients must be between zero and one. A recession coefficient of one gives a fast response. These coefficients usually need to be calibrated.

Model parameters

A few parameters from par.txt need to be mentioned in relation to floodplains.

• The parameter used to calculate the dead volume in the main watercourse, deadm, should not be changed after/if it has been used to determine the thresholds. The parameter, if larger than zero, lets the river hold a water volume after the flow from the river has stopped. This can be important if you simulate substances. It can also delay the start of flow after a dry (zero-flow) period by being filled up with inflowing water replacing evaporated water during the dry period.
• Lake, river and floodplains evaporates according to the value of the evaporation parameters (cevp, ttmp, both land use dependent) for the land use defined for these classes.
• Surface runoff recession coefficient (srrcs, land use dependent) should be set to 1 for lake and river classes with floodplains. Then no water will be left standing on the dry part of the floodplain, but will be added to the flooded water.
• There is a possibility to (temporary) replace the some of the data in FloodData.txt with model parameters (in par.txt). This possibility can be used to (automatically) calibrate the elevation thresholds and recession coefficients. The parameters are general parameters, and thus only one floodplain can be in the set-up or all floodplains in the set-up will have the same parameter values during calibration. The use of this calibration parameters are set with a parameter optonoff, and the parameters are called opt1, .., opt8. Different values for optonoff will replace different sets of floodplain data. You can replace none (optonoff=0) or all of them (optonoff=1), but alternatively replace only thresholds (optonoff=2), only recessioncoefficients (optonoff=3) or only maximum extent of floodplain (optonoff=4).

The parameters are described in par.txt.