Navigation
HYPE Documentation
Quick links to often-used pages:
HYPE links
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
Quick links to often-used pages:
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
For an overview of basic assumptions and explanation of variables see the Basic assumptions section in the Rivers and lakes chapter.
The wetlands that are simulated are small artificial ponds. They have an area and depth (dep), but their area is not taken into account in terms of precipitation and evaporation. The water flow passes through the wetlands without being affected, so it's just as nutrient traps that the wetland model is significant. There are two types of wetlands, just as for the rivers and lakes. They are situated before the river in the calculation scheme. The local wetland (lrwet) receives a share of the local runoff (part) the rest passes by unaffected. Wetlands in main rivers (mrwet) receive a portion of the flow in the main river and the rest passes unaffected.
In wetlands, retention of inorganic nitrogen is modelled (denitrification). For total phosphorus retention (sedimentation) and production (or release from sediments) of TP are modelled. The rates of these processes are constant coefficients (teta=1.2, tkoeff=20, inpar=2.3, sedpar= 0.09, and uptpar=0.1). The retention is limited to 99.9% of the substance in the wetland. The retention (retIN, retTP, g/d) depends on the rate parameter, the concentration in the wetland, wetland area, and for inorganic nitrogen also on 5-day-mean air temperature (T5). The production (prodTP, g/d) depends on a rate parameter, the concentration of the inflow to the wetland, wetland area, and a temperature function (30-day-mean air temperature, T30). The change in TP are divided equally between SP and PP.
| Parameter/Data | File |
|---|---|
| lrwet_area, lrwet_dep, lrwet_part, mrwet_area, mrwet_dep, mrwet_part | GeoData.txt |
| Modules (file) | Procedures |
|---|---|
| npc_surfacewater_processes (npc_sw_proc.f90) | calculate_river_wetland |
| calculate_riverwetland_np |
Arheimer, B. and H.B. Wittgren, 2002. Modeling nitrogen removal in potential wetlands at the catchment scale, Ecol. Eng., 19: 63-80.
Tonderski, K.S., Arhemier, B. and Pers B.C., 2005. Modelling the Impact of Potential Wetlands on Phosphorus Retention in a Swedish Catchment, Ambio, 34(7): 544-551.
The wetlands are water classes, but simulated as a land class with special functions. If the soil is over saturated the standing water is the water volume of the wetland (vol, m3). If the soil is not over saturated, the wetland is dried out. The wetlands area (area, m2) is defined by the class area, and the depth (w) varies with flow. A threshold (w0) for the wetland outflow above the soil surface keep water in the wetland. The wetland outflow is determined by a rating curve above this threshold (see also lake outflow). The thresholds can be set by parameters or if parameters are not set it is equal to minus the streamdepth (from GeoClass).
There are two types of wetlands; internal wetlands (iwet) and wetlands at the outlet of the subbasin (owet). Internal wetlands recieve a fraction (ifraction) of the runoff from other land classes (Figure 1). Outlet wetlands cannot be present in the same subbasin as an outlet lake. They recieve the flow from the main river of the subbasin (Figure 2).
The concentration of the wetland (conc) is the concentration of soil water in soil layer 1. While calculating wetland nutrient processes only the nutrients in the water volume of the wetland in considered though. After that the nutrient concentration of the upper soil layer is updated.
Denitrification of inorganic nitrogen in the wetland is modelled as denitrification in the soil water. Sedimentation of organic nitrogen, particulate phosphorus and suspended sediments are simulated (sed, g/d). Uptake of inorganic nutrients (IN and SP) are modelled as macrophyte uptake. The macrophytes are assumed to cover a part of the wetland area (fracarea). The covered fraction is calculated as the part that is shallower than a production depth (proddep) assuming the wetland area is decreasing linear with depth until twice the average depth of the wetland. The macrophytes are assumed to give residuals of equal amount of nutrient back to the sediment (i.e. immobile organic nutrient pools of soillayer one). The macrophyte uptake process (upt, g/d) depends on a rate parameter (uptpar), macrophyte fraction of wetland area, temperature (tmpfcn) and total phosphorus concentration (TPfunc). The temperature and TP functions are similar to the ones used by primary production in lakes). The temperature function use 5- and 30-day mean air temperature (T5, T30). The half saturation concentration of TP is 0.05 mg/L (hsatTP). The sedimentation is limited to 99.9% of the substance in the wetland water, while macrophytes are limited to 50% of the dissolved inorganic nutrients.
| Symbol | Parameter/Data | File |
|---|---|---|
| ifraction | calculated from iwetcatch | GeoData.txt |
| w0 | streamdepth or iwet0,owet0 | GeoClass.txt or par.txt |
| k | calculated from catchment area parameters wetrate, grata | par.txt |
| p | wetexp | |
| velpar | wlsed | |
| uptpar | wlmphuptin,wlmphuptsp | |
| proddep | wlproddep | |
| tmppar | wltmpexp |
| Modules (file) | Procedures |
|---|---|
| npc_surfacewater_processes (npc_sw_proc.f90) | wetland_substance_processes |
| surfacewater_processes (sw_proc.f90) | wetland_watermodel |
| T2_processes_in_wetland | |
| get_wetland_threshold |
Irrigation constitutes a key water management activity in many parts of the world. Therefore, the HYPE model has a routine to simulate irrigation. The representation of irrigation in the model is based on a set of principles. Firstly, the irrigation water demand is assessed. Subsequently, the demanded water is withdrawn from the defined irrigation water sources. HYPE can either withdraw water from defined sub-basins in the model domain (subject to availability), or from unlimited sources outside the domain. Finally, the withdrawn water is applied onto the classes from which the demand originated. In addition, water losses between demand, withdrawal, and application are taken into account (for withdrawals within the model domain).
A class is irrigated if the crop type associated with it is irrigated (defined in GeoClass.txt). A crop is irrigated if the irrigation input variables in the CropData.txt file are defined and non-zero (plantday, lengthini, kcbini, lengthdev, lengthmid, kcbmid, lengthlate, kcbend, dlref). Irrigation also requires appropriate values in the MgmtData.txt file (gw_part, regsrcid, irrdam, region_eff, local_eff, demandtype) and the par.txt file (pirrs, pirrg, sswcorr etc.). See the File Reference for more details on each file and each parameter.
The irrigation water demand () is calculated each day for each irrigated class (j) at the end of the soil water balance calculations. Two approaches to calculate
are implemented in HYPE, one for submerged crops (e.g. paddy rice) and one for non-submerged crops. The input variables imm_start and imm_end in CropData.txt define (1) the beginning and end of the submerged season, and (2) if crops are submerged or not (zero is interpreted as a non-submerged crop).
For non-submerged crops, the calculations are based on the FAO-56 crop coefficient methods (Allen et al., 1998). The dual crop coefficient method is used because it is more specific than the single crop coefficient method, and more suitable for daily water balance models. Since transpiration is of primary interest in estimating crop water demand, the irrigation routine focuses on estimating potential transpiration () with the basal crop coefficient (
) and the reference potential crop evapotranspiration (
):
ET0 follows the dynamics described above ( here following Wisser et al. (2008)). KCB depends on crop type and phenological stage, which is defined in CropData.txt. KCB is constant during the initial development stage, then increases linearly during the development stage until it reaches the mid-season stage during which it is again constant. Finally,
decreases linearly from the end of the mid-season stage until the end of the season. The dynamics of
and
produces a dynamic
profile (Figure 3). Allen et al. (1998) provide indicative values for
(cf. their Table 17).
The growth season (and irrigation period) start on the plant day (planting). The growth start is determined by a constant (plantday) or depending on climate similar to the options for nutrient uptake. If it is dynamically determined by the degree-day method it is set to the first day of the year which has a degreeday sum (GDD) above a threshold (gsgddsow).
The degreeday sum (GDD) is calculated as
where d is day of year, T is air temperature (degree Celsius), gsbasetemp is a temperature threshold. The GDD is accumulated for each day after gsfirstday with day length larger than gsdaylen. The GDD is reset to zero at gsfirstday.
Another alternative is for it to be dynamically determined by the temperature threshold method. It is then set to the first day after a given earliest day (gsfirstday) which has consecutive number of days (gsaccdays) with daily mean air temperature above a threshold (gsdaytemp).
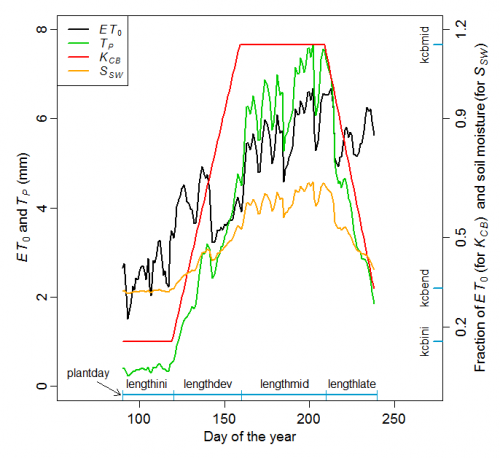 |
| Figure 3 Illustration of |
On any given day, the model first calculates whether irrigation is needed, and then the amount required. The irrigation need is assessed by comparing the current soil water content (H) with a dynamic irrigation threshold (, the soil water stress threshold):
H is the plant-available soil moisture (i.e. soil water above wcwp1 and wcwp2 in soil layers 1 and 2 respectively). AWC is the maximum plant-available water content in soil layers 1 and 2 (i.e. the sum of fc1 and fc2). is a fraction of AWC (defined upwards from wcwp). Below
the crop experiences water stress, creating a need for irrigation.
varies from day to day and depends on the crop type and
:
is a crop-type specific reference depletion level (essentially the fraction of AWC that can be depleted before stress occurs, defined downwards from wcfc). Allen et al. (1998) provide indicative values for
(cf. their Table 22). The
equation is a slightly modified form of the original FAO-56 equation to account for the fact that only
is used here. A typical
profile is shown in Figure 3. By default,
is limited to the range 0.2 – 0.9, but it can be further refined with the parameter
(sswcorr in par.txt) to maximum 1.
If irrigation is needed, the required irrigation amount () can be calculated with three alternative methods in HYPE (chosen by the demandtype variable in MgmtData.txt):
(1) A constant (defined by the irrdemand parameter in par.txt)
(2) Up to the field capacity:
(3) Up to a defined fraction of (
, iwdfrac in par.txt):
The fraction can be larger than 1. For example, to irrigate to a level 10% above ,
=1.1.
is, however, limited to
.
The irrigation of submerged crops aims to satisfy a target flooding level above the soil surface (Wisser et al., 2008). The target flooding level is a constant input parameter (, immdepth in par.txt).
Irrigation is required if the water level of the top soil layer (H1) falls below the target flooding level:
The irrigation water demand is equal to the amount needed to reach the target flooding level:
If the submerged season is shorter than the crop season, during the non-submerged period is calculated in the same way as for non-submerged crops. To maintain a desired flooding level and simulate terracing, for example, it may be necessary to adjust the soil and runoff parameters of the class with the submerged crops.
When
has been calculated for each irrigated class in the sub-basin, the total field-scale irrigation water demand for the sub-basin (
) is calculated:
Irrigation water can be abstracted from a set of water sources (Figure 4). Within a given sub-basin, water can be abstracted from the olake, the ilake, the main river, and from groundwater in a deep aquifer. In addition, water can be withdrawn from the olake and the main river of another sub-basin. These sources can be used on their own or in combination. Alternatively, HYPE can withdraw water from an unlimited source outside the model domain. This is specified with the irrunlimited code word in info.txt, and applies to all irrigated sub-basins.
Withdrawals are calculated directly after the local discharge and the upstream discharge has been combined to flow into the main river of a given sub-basin.
Before any withdrawal occurs, the field-scale is scaled to sub-basin scale (
, the local sub-basin irrigation water demand). This is done in order to account for the often significant water losses between withdrawals and soil moisture replenishment. A simple user-provided scaling factor is applied:
The local efficiency (, local_eff in MgmtData.txt) represents the fraction of the withdrawn water within the sub-basin that infiltrates the irrigated soil.
accounts for losses in irrigation canals, ponds etc. within the sub-basin, and for on-field losses from irrigation equipment (e.g. sprinkler systems).
is not scaled if all withdrawals are from an unlimited source outside the model domain (i.e.
if
irrunlimited is y).
The model first attempts to withdraw water from sources within the sub-basin where the demand originated. The user specifies the proportion of water to be withdrawn from surface water and deep aquifer groundwater sources, respectively, in the MgmtData.txt file (gw_part). A gw_part value between 0 and 1 represents the long-term average proportion of surface and deep aquifer groundwater withdrawals for irrigation within the sub-basin. A gw_part value of 0 indicates that all irrigation water exclusively comes from surface water sources, while a gw_part value of 1 indicates that all irrigation water exclusively comes from deep aquifers. Based on gw_part, is split into the groundwater demand (
), and the surface water demand (
).
If any surface water demand exists, the model sequentially attempts to withdraw water from the olake, the ilake, and the main river. However, water withdrawal from olakes and ilakes is only calculated if the variable irrdam in MgmtData.txt is set to 1 for the sub-basin. Water withdrawals from the main river occur both from the inflow to the river reach and from the volume stored in the reach.
If the volume is available at the source, the demanded water is withdrawn. Otherwise, only the available volume (
) is withdrawn. The withdrawal is scaled with the user-defined parameter
(pirrs in par.txt):
where is the abstracted water from the first surface water source in the sub-basin, and
is the residual surface water demand. The residual demands (
and below
,
and
) are calculated without the
scaling in order to prevent erroneous source compensation due to scaling. If any demand remains, the next surface water source is probed in the same manner:
The total surface water withdrawal within the sub-basin (), and the remaining surface water demand (
) is calculated accordingly, based on the abstractions from each source (k):
If any groundwater demand exists, the model withdraws a user-specified fraction of from an unlimited source outside the model domain or if an aquifer is simulated connected to the subbasin from this aquifer. The first case conceptually represents a large deep aquifer source, which is currently outside of the model domain.
is the abstracted groundwater and
(pirrg in par.txt) is the groundwater withdrawal scaling:
To simulate a more dynamic conjunctive use of groundwater and surface water sources, the model allows for compensation of remaining surface water demands from the groundwater source. This compensation is only allowed if both groundwater and surface water sources are used (0<gw_part<1), and if the irrcomp parameter is >0. The irrcomp parameter defines the degree of compensation allowed, i.e. the fraction of the residual surface water demand which can be met through source compensation. The compensation algorithm is as follows: if any surface water demand remains ( > 0) and the groundwater is not depleted, the groundwater withdrawal cycle is calculated once more using the scaled residual surface water demand. Finally, after possible source compensation, the remaining (surface) water demand at the sub-basin scale (
) is calculated.
The model can also simulate withdrawal from another sub-basin in the model domain (, defined with the regsrcid input variable in MgmtData.txt). This withdrawal is calculated when the model reaches
in the calculation order, after possible local irrigation water abstractions in
and only if any irrigation demand remains in the sub-basin(s) connected to the regional source (
> 0).
For each connected sub-basin (i),
is scaled to represent the regional-scale demand from that sub-basin (
). Again, a simple scaling factor is applied:
The regional efficiency (, region_eff in MgmtData.txt) represents the fraction of the withdrawn water at the regional source that reaches the connected sub-basin.
refers to the connected sub-basin. The regional scaling accounts for often significant water conveyance losses in large irrigation networks (in canals and dams etc.).
The total water demand from the regional source () is then calculated as the sum of the demand from each connected sub-basin, scaled by a parameter controlling the strength of the regional connection (
, regirr in par.txt):
The regional demand can be met from two sources in sub-basin : the olake and the main river. If the regional source sub-basin has an olake, and if the irrdam input variable is set to 1 for that sub-basin, the model attempts to withdraw
first from the olake and then the residual from the main river. If not, the model only attempts to withdraw
from the main river. The regional abstraction (
) is limited by the volume available at the source (
) and the scaling parameter
:
where is the abstracted water from the first water source in
,
the volume available at the first source,
the residual regional water demand after withdrawal from the first source (but prior to the
scaling),
the abstracted water from the second water source in
, and
the volume available at the second source.
The concentrations of the withdrawn water are the same as that of the irrigation water source. If the water originates from several sources, the volume-weighted concentration is calculated. If desired, the model can simulate sedimentation tanks, in which a defined fraction of the particulate phosphorous (pp) and organic nitrogen (on) settles:
where is the concentration of the abstracted water after settling,
is the concentration of the source, and
is the concentration reduction fraction (cirrsink parameter in par.txt). To use sedimentation tanks in a region, the concentration reduction fraction needs to be set in par.txt (0<cirrsink≤1).
If the model withdraw water from an unlimited source outside the model domain, the concentration of the water applied is assumed the same as the concentration of the recieving soil layer. Thus the concentration is assumed not to be affected by the irrigation.
In the calculation order, the irrigation water application occurs the next time step the model reaches the sub-basin from which the demand originated (typically the following day). The water is applied to the soils at the beginning of the soil balance calculations, before the calculation of the natural processes.
The regionally abstracted water () is first distributed to each connected sub-basin (i) according to their proportional demand, and then scaled to the local scale using the respective regional efficiency:
For a given sub-basin, the total amount of abstracted water available at the local scale () is calculated and then scaled, using the local efficiency, to represent the water applied to the soil (
):
is then distributed onto each irrigated class in proportion to its water demand:
is added to the soil water of class j as additional infiltration.
is added to the top soil layer. The soil layer may then hold more water than the pore volume of the soil layer. This will percolate into lower soil layers together with rain if the water is above field capacity. For unlimited irrigation:
,
and
.
The water withdrawn from a regional source that does not reach connected sub-basins () evaporates at the regional source (
):
Similarly, water losses due to local inefficiencies () evaporate within the sub-basin itself. This applies to local losses from abstractions both within the sub-basin and from the regional source (where applicable):
Evaporation due to regional and local inefficiencies proportionally concentrates substances in the withdrawn water. The substance concentrations in the irrigation water applications are hence higher than at the points of withdrawal (the mass remains the same while the volumes are reduced). However, if unlimited irrigation is simulated, the concentrations of the applied water are the same as in the layers to which water is added (i.e. causing no change in concentration).
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| cropid, reg | CropData.txt | ||
| mgmttype=1, subid | MgmtData.txt | ||
| Irrigation water demand | imm_start, imm_end | CropData.txt | |
| Non-submerged crops | demandtype | MgmtData.txt | |
| planting set or calculated from: | plantday, gsdaylen, gsgddsow, gsbasetemp, gsdaytemp, gsaccdays | CropData.txt | |
| planting, lengthini, kcbini, lengthdev, lengthmid, kcbmid, lengthlate, kcbend | |||
| dlref | |||
| sswcorr | par.txt | ||
| iwdfrac | |||
| AWC | wcfc1+wcfc2 | ||
| Submerged crops | wcwp1, wcfc1, wcep1 | par.txt | |
| immdepth | |||
| Irrigation water withdrawal | irrunlimited | info.txt | |
| Irrigation inefficiencies within the sub-basin | local_eff | MgmtData.txt | |
| Withdrawal from sources within the sub-basin | irrdam, gw_part | MgmtData.txt | |
| irrcomp | par.txt | ||
| pirrs, pirrg | |||
| Withdrawal from another sub-basin | regsrcid | MgmtData.txt | |
| region_eff | |||
| regirr | par.txt | ||
| Substance concentrations of irrigation water withdrawals | cirrsink | par.txt |
| Modules (file) | Procedures | Section |
|---|---|---|
| irrigation_module (irrigation.f90) | calculate_irrigation | irrigation water withdrawal |
| irrigation water application | ||
| apply_irrigation | irrigation water application | |
| irrigation_abstraction_sink | substance concentrations of irrigation water withdrawals | |
| calculate_irrigation_water_demand | irrigation water demand | |
| calculate_kcb | ||
| irrigation_season | ||
| immersion_season |
Allen, R.G., L.S. Pereira, D. Raes, and M. Smith 1998. Crop Evapotranspiration (guidelines for computing crop water requirements), FAO Irrigation and Drainage Paper, No. 56, FAO, Rome, Italy, 300 pp.
Wisser, D., S. Frolking, E.M. Douglas, B.M. Fekete, C.J. Vörösmarty, and A.H. Schumann, 2008. Global irrigation water demand: Variability and uncertainties arising from agricultural and climate data sets, Geophysical Research Letters, Vol. 35, L24408, doi:10.1029/2008GL035296, 5 pp.
Information on point sources is located in the file PointSourceData.txt. Point sources can be added to the model in different ways. They can be added as a constant source each time step, or with a constant that is changing some times during the simulation. They can also be added as time series of flow and concentration. For the first case all information of the point sources is found in the PointSourceData.txt file. For the second case the time series are given separate, and the file holds information on where the point sources are located. Simulated substances not having an concentration given in the file(s), will have concentration zero (default). This may be inappropriate for T2, water temperature.
The model can handle up to three different types of point sources. They can used to simulate e.g. treatment plants, stormwater outlets, and industrial sources as separate types. All point sources have a constant flow, concentrations of total nitrogen and phosphorus, and fractions of IN and SP for a period of time. The time may be the whole simulation period, or different sources may be active during different parts of the simulation period. Point sources are added to the water in the main river.
Sediment point sources are handled similar to nutrient point sources. A point sources has a constant flow, concentration of total suspended sediment (TS), and fraction of suspended sediments (SS). The point source may be active the whole simulation period, or different sources may be active during different parts of the simulation period. Point sources are added to the water in the main river.
Water temperature may be added to the flow of nutrient and sediment point sources if T2 is simulated together with N and P. Water temperature point source may also be added on its own in the same way as tracer T1 in different locations of the river network.
Tracer T1 point source may be added in the same way as nutrient and sediment point sources. In addition, point sources of tracer T1 can be added to the local stream, the local lake, the main river or the outlet lake.
Time series of point sources can be given in special file. In this case the PointSourceData.txt holds only information on which point sources exist in the model and where they can be found.
The model can handle up to three different types of point sources. They can used to simulate e.g. treatment plants, stormwater outlets, and industrial sources as separate types. The point sources are given as either daily, monthly or yearly time series. They are given a flow and a concentration for each nutrient species simulated, i.e. IN, ON, SP, PP, AE or SS. Point sources are added to the water in the main river.
Water temperature may be added to the point source flow the same way as concentration.
Tracer T1 point source may be added to the point source flow the same way as other concentrations.
A point source with “negative flow” denotes an abstraction of water. The abstraction of water can be made from four different locations. The default is to remove it from the main river volume (including the queue) after all river processes have been calculated except outflow from the river. Alternatives are to abstract the water from the outlet lake volume, from an aquifer or from the main river inflow from upstream and from the river volume (and queue) proportionally. In the latter case the removal is done before any inflow to the main river is added (e.g. from upstream, point sources, or precipitation). The water is removed from the source, while the concentration is kept.
Negative point sources can be constant or periodically constant abstractions by giving a negative flow (a negative value). Alternatively they can also be given as time series. In the latter case the flow time series is positive but it is defined as a negative point source in PointSoureData.txt.
| Section | Parameter/Data | File |
|---|---|---|
| Constant or periodical point sources - Nutrient | subid, ps_vol, ps_type, ps_tpconc, ps_tnconc, ps_infrac, ps_spfrac, fromdate, todate | PointSourceData.txt |
| Constant or periodical point sources - Sediment | subid, ps_vol, ps_type, ps_tsconc, ps_ssfrac, fromdate, todate | |
| Constant or periodical point sources - Tracer T2 | subid, ps_vol, ps_type, ps_t2, fromdate, todate | |
| subid, ps_vol, ps_type=0, ps_t2, fromdate, todate, ps_source | ||
| Constant or periodical point sources - Tracer T1 | subid, ps_vol, ps_type, ps_t1, fromdate, todate | |
| subid, ps_vol, ps_type=0, ps_t1, fromdate, todate, ps_source | ||
| Time series point sources | psid, subid, ps_type, ps_source | PointSourceData.txt and PSTIMESeries.txt |
| Negative point source | subid, ps_vol, fromdate, todate, ps_source | PointSourceData.txt |
| psid, subid, ps_source | PointSourceData.txt and PSTIMESeries.txt |
| Modules (file) | Procedures |
|---|---|
| datamodule (data.f90) | load_pointsourcedata |
| read_pointsourcedata | |
| get_current_pointsources | |
| npc_surfacewater_processes (npc_sw_proc.f90) | add_point_sources_to_main_river |
| surfacewater_processes (sw_proc.f90) | point_abstraction_from_main_river |
| point_abstraction_from_outlet_lake | |
| tracer_processes (t_proc.f90) | add_tracer_point_source_to_river |
| add_tracer_point_source_to_lake |
Water transfer can be simulated by HYPE in different ways. One way is to represent abstraction by defining negative point source discharge. Another method is to use the bifurcation functionality that defines a branch through which the water is transferred to a downstream receiving subbasin. A third way is to define water transfer through water management (abstracting from subbasins with outlet lakes and transferring to any other subbasin). The negative point source method has the disadvantage as a water transfer that the concentration of the water is specified by the user and not the concentrations of the water abstracted, but the abstraction can be located at different points throughout the catchment. The bifurcation method has the limitation that the receiving subbasin must be downstream. The management method can only take water from an outlet lake, and the water transfer will be delayed one time step. In all methods, the amount of water available on any given day will limit the amount that can be withdrawn or transferred.
Water transfer through bifurcation lets you divert a part of the outflow from a subbasin through a branch to another downstream subbasin specified in BranchData. The flow diverted may be defined by BranchData parameters (fraction, max-, or minflow). The water transfer can alternatively be given as a recorded time series of demanded water transfer (given as dwtr in Xobs). This water will then be taken from the ordinary simulated outflow of the subbasin if there is enough flow, the remaining flow will go through the main channel. A third method, if you have an outlet lake, is to use two outlets. The flow of outlet 2 can be defined as the flow given by dwtr.
See also the general description of bifurcations and Outlet lake with two outlets.
Abstraction of water can be defined as a negative point sources. The abstracted water may be constant (or constant at different values for different periods), and thus the same amount of water is removed from the model every time step or given as a time series. The abstraction can be made from different points in the river network within the subbasin. The water is removed while the concentration is kept in the water remaining in the river. To simulate water transfer within the model domain, the same amount of water need to be added as a (positive) point source in another subbasin. This subbasin do not have to be downstream, since its (constant) flow and concentrations is defined in the file beforehand. However, there is no direct connection between the subbasins in which water is abstracted and released, respectively. In order to preserve the water balance, the user must define equally large flows abstracted and added. Since the concentration of the negative point source is defined in the file beforehand, the connection to the quality of the water abstracted water is not automatically preserved.
Water transfer between two subbasins can be defined through water management (MgmtData.txt) if the source is an outlet lake. The source subid and subid of the receiving subbasin is defined together with a constant flow. The water is taken from the outlet lake of the source subbasin and is given the concentration of the lake. The water is then transported to the other subbasin's main river and arrive there the next time step. The delay in flow is necessary to handle transfer upstream within a catchment. Several water transfer can be specified for the same source or recieving subbasin.
Alternatively a demanded flow time series from Xobs can be used instead of a constant flow. In this case only one water transfer can be specified for each source lake.
| Section | Parameter/Data | File |
|---|---|---|
| Water transfer through bifurcation | ALL | BranchData.txt |
| ldtype=5 and 6 | LakeData.txt | |
| lakeid, rate, exp, deltaw0, qprod1, qprod2, datum1,datum2, qamp, qpha, regvol, maxQprod, minflow, obsflow | ||
| dwtr | Xobs.txt | |
| Water transfer through negative point source | ps_vol, fromdate, todate, ps_source | PointSourceData.txt |
| psid, subid, ps_type, ps_source | PointSourceData.txt and PSTIMESeries.txt | |
| Water transfer through water management | mgmttype=2 | MgmtData.txt |
| subid, receiver, flow | ||
| dwtr | Xobs.txt |
| Modules (file) | Procedures | Section |
|---|---|---|
| datamodule (data.f90) | load_pointsourcedata | negative point source |
| load_management_data | water management | |
| npc_surfacewater_processes (npc_sw_proc.f90) | add_point_sources_to_main_river | negative point source |
| surfacewater_processes (sw_proc.f90) | calculate_outflow_from_outlet_lake | bifurcation |
| point_abstraction_from_main_river | negative point source | |
| add_point_sources_to_main_river | ||
| point_abstraction_from_outlet_lake | ||
| add_water_transfer_to_main_river | water management | |
| water_transfer_from_outlet_lake |
Regulation of flow through dams is described in the Chapter about Rivers and lakes. Dams of different purposes and regulation management can be simulated. See details in the sections on Simple outlet lake or dam and the special case of an Outlet lake with two outlets.