Navigation
HYPE Documentation
Quick links to often-used pages:
HYPE links
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
Quick links to often-used pages:
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
The HYPE model simulates most lakes and rivers in a conceptual way. The HYPE model can contain two types of rivers, local river and main river, and two types of lakes, local lakes and outlet lakes (Figure 1). The local river represent all ditches, streams, rivers within a subbasin that recieve only runoff within the subbasin. It is modelled as one conceptual river with a length, regardless of the actual distance runoff from different land has to travel through the subbasin. Similarly a local lake represents all lakes within a subbasin receiving inflow only from within the subbasin. The modelled local lake recieves a fraction of the flow in the local river. The fraction is defined as a fraction of the subbasin area. The main river is the river part(s) of a subbasin that water from upstream subbasins flows through. Depending on subbasin delieation it may be clearly defined or represent several tributaries that comes to the subbasin outlet. Finally the modelled outlet lake represents a lake located at the outlet of a subbasin.
A local stream and a main rivers are present in all subbasins as default, and the length of each watercourse is then calculated as the square root of the subbasin area. River lengths can be given as input, and then their value decide if there will be a stream or river in the subbasin. If the river length is zero no river is calculated. The river can be defined as a SLC class and has then an surface area in addition to a length, but rivers can also be without area (i.e. no fraction of the subbasin area are occupied by the river and no precipitation added to the river).
All runoff from land enters the local river. Local lakes (ilake) receive a portion of the local flow. The flow leaving the local river and the outflow from local lake, goes to the main river of the same subbasin. If there are upstream subbasins their flow is added to the main river together with the local flow. Outlet lakes (olake) receive the outflow from the main river, i.e. all upstream and local flows.
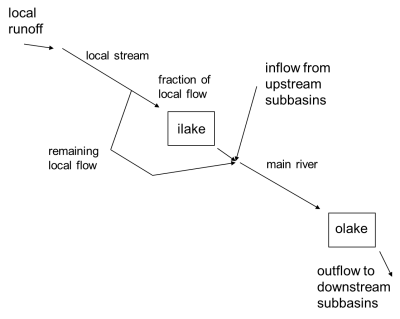 |
| Figure 1: Schematic representation of streams and lakes in a subbasin of HYPE, and the links between them. |
The two lake types are separate classes. The lake classes have characteristics such as land use and soil type, which are defined together with the other classes' characteristics (in GeoClass.txt). Precipitation, atmospheric deposition and evaporation of rivers and lakes are calculated first, while river flow and inflow, transformation processes and the outflow of the lakes is calculated thereafter. Lakes and rivers are calculated in the model’s routing part after all classes are calculated for the subbasin.
An outlet lake can be part of a larger lake. It is then called a lake basin. Lake basins are olakes in nearby subbasins.
A simple outlet lake has a threshold. If the water level drops below the threshold, the outflow ceases. Lake mean depth below the threshold is specified in GeoData.txt or LakeData.txt as lake_depth in meters. Lake depth can also be set by parameters, i.e general parameter gldepo or olake region parameter olldepth. At the start of a simulation the water depth of the lake is set to be at the threshold. The current water depth, denoted wlm in Fig. 2, can be above or below the threshold.
For output, the outlet lake water level (output variable wcom) is given in a user set reference system. The reference level is used to get the same height system as any observations of the lake's water level. It uses the unit of meter, and the reference level (w0ref) gives the level of the threshold in the reference system (Fig. 2). The output wcom is calculated as the water level above the threshold plus w0ref. A regulated lake (dam) has two thresholds. The distance between the thresholds are determined by the regulation volume (regvol) of the dam with the assumption that the dam has constant area with depth. In reality the area may decrease with depth. This means that the the observed variation in water level may be larger than the simulated variation. It is therefore possible to adjust the output wcom (and wcav) with the actual amplitude of the regulation volume (wamp). This will make the simulated and recorded water stage comparable below the upper threshold for a regulated lake.
A local lake also has a threshold depth that is used as start value. The depth is given by general parameter gldepi and is then the same for all the local lakes, or by ilake region parameter illdepth. It is measured in meters. A percentage of flow from the local stream flows into the local lake. The rest of the local flow runs directly to main river watercourse.
The streams may have a delay and an attenuation of the flow. The former shifts the peaks, but leaves them otherwise untouched, while the attenuation both delays and smooths out peaks. The streams have a dead volume in which the residence time of solutes is increased relative to the water and the concentration smoothed out further over time.
| Parameter/Data | File |
|---|---|
| rivlen, loc_rivlen, slc_nn | GeoData.txt |
| special class code 1,2,11 and 12 | GeoClass.txt |
| lake_depth | GeoData.txt or LakeData.txt or DamData.txt |
| gldepo, olldepth, gldepi, illdepth | par.txt |
| w0ref, regvol, wamp | LakeData.txt or DamData.txt |
| Modules (file) | Procedures |
|---|---|
| modelmodule (model_hype.f90) | initiate_model_state |
| initiate_model | |
| calculate_flow_from_undivided_lake | |
| calculate_flow_for_lakebasin_lake | |
| surfacewater_processes (sw_proc.f90) | calculate_riverlength |
| calculate_ilake_outflow | |
| calculate_outflow_from_outlet_lake | |
| calculate_outflow_from_lakebasin_lake | |
| remove_outflow_from_lake | |
| calculate_branched_flow |
Daily precipitation is added to the river if it has an area (is a class) and a new concentration is calculated. Precipitation is divided between river water in damping box and queue according to the respective volumes.
If the river has an area (as a class), it evaporates and a new concentration is calculated. The river is assumed to evaporate at potential evaporation rate (see Processes above ground - Evaporation). Normally the river area is constant over time, but with parameters a reduction of riverarea can be simulated for low volume/flow. The reduced river area is also used for heat exchange calculations.
The parameters fraxe and fraxm are general, and fraxe is (minimum) mean river depth (m) where fractional river area = 1 and fraxm is mean river depth (m) where the slope of the fractional river area has its maximum (must be in the range between 0 and fraxe). x is the current mean river depth (estimated as river water volume (including possible deadvolume) divided by the full area extention).
The delay in the watercourse (transtime) in days is determined by the length of the watercourse (rivlen) and the water’s maximum velocity (rivvel). The maximum velocity is a general parameter with unit m/s. The delay in the river is dependent on subbasin land area if the default river length is used. The delay is a pure translation unless the parameter damp is set. The pure delay is divided into whole days (ttday) and parts of the day (ttpart) (if the time step is daily, other wise the division is made into whole and fractions of that time step). In the following description daily time step is assumed.
The inflow of the river is stored in two arrays (riverq and riverc) until it is time for it to flow out of the river stretch. The outflow is weighted by using the parts of the time step (ttpart) that are to flow out during the time step.
transq = (1-ttpart)*riverq(ttday) + ttpart*riverq(ttday+1)
IF(transq>0)THEN
transc = ((1-ttpart)*riverq(ttday)*riverc(ttday) +
ttpart*riverq(ttday+1)*riverc(ttday+1)) / transq
ELSE
transc = 0.
ENDIF
After the calculation of outflow the values in the arrays are shifted forward one time step.
If the delay in the watercourse also includes a damping of the peaks then only part of the delay is considered as translation, while the rest of the delay lies in damping. The translation is calculated first and then the flow goes through a linear box that creates attenuation. The parameter damp indicates how much of the delay that will occur in the attenuation box (or damping box), and translation time is reduced accordingly. Otherwise the translation is calculated in the same manner as above.
The result from the translation of water (transq and transc) flows into the attenuation box, which is assumed to be completely mixed. The delay time in the box (kt, in timesteps) is determined form input and parameters.
The outflow equation depends on the attenuation box's volume before changes during the time step () and on the net inflow during the timestep (inflow). The net inflow includes the outflow from the translation (local runoff, upstream inflow, point sources etc.), removal though irrigation or regional groundwater flow, and the flow to or from a main river floodplain. The equation has two coefficients:
An earlier version of calcuation of outflow from the box can be accessed through a model option. In this case the delay time of the attenuation box is recalculated to a recession coefficient (riverrc). The recession coefficient is used to calculate the outflow from the box (dampq) by the current volume in the box (riverbox).
where .
A dead volume (deadriver, ) can be used to get additional equalization of concentrations in the watercourse. In this case, the initial value of the attenuation box is equal to the dead volume. Inflows into the box are mixed with the entire volume. At present this represents a dilution of the concentration since the initial value of concentration in the box is zero. In HYPE the dead volume is estimated from the upstream area (including the area of the subbasin itself). This gives the dead volume:
where the parameter dead (deadl or deadm, ) is general parameters, the upstream area uparea (
) is calculated from input data, and the river length (rivlen, m) is estimated to be the root of the subbasin’s area unless it is set among the input data. Dead volume can be used without suppression of water flow peak (damp = 0). When additional smoothing is used, the riverbox in the attenuation equations above is replaced by the volume of the attenuation box minus the dead volume.
In addition, the dead volume is used to calculate a minimum river width used for calculation of river surface area in the case the river area is not given as a class area. The width is assumed to be 10 times the depth and together with the dead volume and river length, the with is calculated as:
The continuous-time equation for the change in volume S in a reservoir is:
where i(t) is influx and q(t) is outflow. If we assume that the outflow is proportional to the volume we get another expression for the change in S. k is in the unit of time.
Combining these two equations gives a first degree equation that can be solved using the method of “integrating factor”:
In our case, we have a constant influx during a time steps of length 1 day. Assume that the influx during a time steps are I and the outflow Q. These flows are thus the equivalent discrete flows. Because I is constant during the time step (i(t) = I) Q can be calculated. Define and integrate the second equation above, from 0 to t (t = 1, one time step).
Calculate Q for time step (the mean of q(t)) and replace the outflow with the volume.
or separated for I and S.
Common in HYPE is that outflows are calculated with a recession coefficient. Here the recession coefficient is defined as the proportion of outflow after an inflow pulse. It is therefore calculated as under the assumption that the starting volume can be neglected, S(0)=0.
For a real flow the volume can of course not be neglected in this way and this relationship is only approximate.
Alternatively the outflow may be calculated from the equation separated for I and S. For this option I is calculated as the sum of several different types of inflow and outflow to the river during the time step, e.g. precipitation and evaporation, in addition to the lateral inflow. In addition the initial value of the river volume (S(0)) is saved here to be used for the outflow calculation.
Bank-full flow is used for calculation of erosion of sediment and particulate phosphorus in rivers (see Sedimentation/Resuspension). This flow has a probability of app. 0.5% (Nixon, 1959). It is in HYPE estimated by the second highest daily flow during the last 365 days, which has similar probability (Rosberg, 2003).
The local river has a length equal to the square root of the subbasin area, if not specified as input. Runoff from the land area of the subbasin forms the inflow to the local river (Figure 3). The flow in the local river is delayed and attenuated as described above. Of the resulting flow from the stream a constant percentage goes to the local lake (icatch), and the rest directly to the main river.
A main river is present in all subbasins. The length is equal to the square root of the subbasin area, if it is not specified as input. In areas without incoming water from upstream there is still a main river, but it receives only local river flow after the local lake. In subbasins with upstream incoming water, the flow to the main river will be the sum of outflow from the local lake, the proportion of flow in the local river not flowing into the local lake and the water from upstream (Figure 4). For a subbasin with a (part of) a multi-basin lake, the main river transports the flow from land to the lakebasin of the subbasin.
The return flow from an aquifer is added to the inflow of the main river (Figure 4).
The flow in the main river is delayed and attenuated as described above. The resulting effluent from the river flows to the outlet lake or to the next subbasin if there is no outlet lake.
If the main river length is zero, the inflows to the main river is added to form the main river outflow.
In input files it is given to which subbasin(s) the outflow from each subbasin flows. The upstream flow enters the main river of the downstream subbasin. Inflow into the main river of a subbasin is calculated by adding outflows from upstream areas. Concentrations are flow-weighted by their relative share. The upstream flow enters the main river, except if the upstream subbasin has a lakebasin that is part of the downstream subbasin's lake. In this case the upstream lakebasin outflow goes directly into the downstream lakebasin.
River diagnostic variables can be calculated for the main river. A river water depth (d) and river velocity (u) can be calculated from hydraulic geometry for the main river and the calculated main river flow (q). In the case of updating of flow in a subbasin with no outlet lake, the updated (main river) flow is used. The equation coefficients are general parameters (c,f,k,m).
Given a continous monotonous increasing equation for calculating water level from flow, the water level of a river (wr) can be calculated from the flow by the inverse of this rating curve. This method is used to calculate main river water level in HYPE. Three different types of river rating curve formulations can be used (TYPEofRRC).
The first is a single rating curve with a threshold (w0) and the rating curve coefficients are input. The rating curve
give coefficients a and b for the inverse equation:
The second type uses two rating curves with the same threshold (w0); one for ice free condition and one for use when there is ice on the river. The transition between the rating curves is smoothed by scaling of the curves in a transition period. The scaling of rating curve parameters are determined by ice porosity and ice thickness (general model parameters). Between thresholds the influence of the ice curve increases linearly from zero to one. The minimum influence (of porosity and thickness) is used as the scaling weight of the winter curve during the transition period. If only parameters for the ice free curve are given as input, the same parameters is used for ice conditions except for the exponent (p) which is then set to one.
The third type is for a sectorial rating curve. It has different rating curve coefficients for different sections of water level. The sections may not overlap or leave gaps in water level, even though small discrepancies is handled. The parameters and sections need to be chosen so that the whole curve is continous. Since the rating curves are used inverted in the code, the sections are turned into sectors of flow. The average of the flow given by the minimum water level of one curve and the maximum water level of another curve is taken as the actual limit between the two curves. This type does not handle ice curves.
In addition to river water level described above, it is possible to calculate the water level in the scale of the local gauge. This could e.g. be in cm and with the zero of the gauge at other location than w0 of the equation. Figure 5 below show the relation between the different parameters.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| Common rivers processes | rivlen | rivlen, loc_rivlen | GeoData.txt |
| fraxe, fraxm, rivvel, damp | fraxe, fraxm, rivvel, damp | par.txt | |
| dead | deadm, deadl | ||
| Local river | icatch | GeoData.txt | |
| gicatch, illicatch | par.txt | ||
| Main river | maindown | GeoData.txt | |
| branchid | BranchData.txt | ||
| c, f, k, m | hygeomc, hygeomf, hygeomk, hygeomm | par.txt | |
| ricew0por, ricew1por, ricew0ice, ricew1ice | |||
| k, p, w0 | k, p, w0ref | RiverRatingCurveData.txt | |
| wmin, wmax, gaugezero |
| Modules (file) | Procedures | Sections |
|---|---|---|
| modelmodule (model_hype.f90) | initiate_model_state | rivers |
| initiate_model | ||
| initiate_model | local river | |
| main river | ||
| surfacewater_processes (sw_proc.f90) | add_precipitation_to_river | precipitation |
| calculate_river_evaporation | evaporation | |
| translation_in_river | pure delay | |
| calc_qbank | bank-full flow | |
| update_qbank | ||
| river_water_level | main river | |
| local_water_level | ||
| ice_on_river |
Nixon, M. 1959. A study of the bank-full discharges of rivers in England and Wales. Journal of the Institute of Civil Engineers 12:157-174.
Rosberg, J. 2003. Modelining phosphorus transport and retention in river networks. Master Thesis. Dept. of Earth Sciences, Uppsala University.
Daily precipitation is added to the lake and a new concentration is calculated. Lakes are assumed to be completely mixed.
The lake is assumed to evaporate at potential evaporation rate (see Processes above ground - Evaporation) and a new concentration calculated. The actual evaporating area is reduced if the lake is (partly) ice covered. Ice is calculated in case water temperature (substance T2) is simulated.
The rating curve is used for calculation of outflow in different circumstances. It is based on water level above a threshold.
In the program the equation is solved for the average flow during the timestep with linearization (Lindström, 2016). For rating curve exponent equal to one, the solution is exact, while for other exponent an approximation is used. The outflow of the lake is limited to the water above the threshold, in the case that the rating curve give a higher value.
The local lake has an initial volume which is determined by its area and threshold depth. The lake depth below the threshold is determined by model parameters (gldepi or illdepth).
The inflow to the lake is a percentage of the flow in the local stream (icatch). The percentage is determined by the percentage of the subbasin area that drains to the lake. This percentage can be given as a fraction in GeoData.txt for each subbasin with an internal lake, or be given by a regional parameter ilicatch, or be given by a general parameter gicatch. If not set at all the default value is 1, i.e. the local river runs through the local lake. The flow from the local river is added to the lake (Figure 6). The lake water is assumed completely mixed.
Water outflow is calculated with the universal rating curve using general or region specific model parameters.
The above description of the functioning of an internal lake (ilake) in HYPE can be changed with a modeloption for connectivity. The default ilake model has no connectivity model. There are two alternatives for introducing lake connectivity within a subbasin. The first is a fill and spill model for a chain of storages. The second is a the Hysteretic Depressions Storage model (HDS). You can choose to use one or the other or to have different ilake descriptions for different subbasins.
This ilake connectivity model simulates the ilake as a chain of small connected lake sections (lks) with different height of their outflow threshold. Depending on water volume in the ilake one or several of the lake sections can be disconnected from the chain (zero outflow with water level below the threshold). The precipitation and evaporation are divided by the lake sections depending on their fraction of the ilake area, but the runoff from land area is divided by the lake sections depending on their fraction of the catchment area. In case the water level of a lake section is above its threshold, its outflow is calculated. The outflow of each lake section is calculated using the universal rating curve using general or region specific model parameters same as a simple ilake. The outflow of a lake section is of course also added to the receiving lake section before that one’s outflow is calculated. Depending on how far upstream from the last lake section of the chain there is inflow from the above lake section, that fraction of the ilake area is the ilake’s current connectivity. The catchment area of the lake sections above this border is the currently non-contributing catchment area.
Another model for the local lake is the Hysteretic Depressions Storage (HDS) model (Ahmed et al. 2023, Shook et al. 2021). The HDS model does not simulate depressions as distinct (individual) depressions, rather, it simulates the effects of the integrated depressions system and their connection at the basin level as a lumped depression storage (ilake). The HDS model simulates the change in the contributing area, depressional storage, and outflow from the subbasin.
The model has contributing area fraction as a state. The runoff from the contributing area is outflow from the HDS model of the subbasin. The non-contributing area fraction of runoff is added to the depression storage. If the water of the depression is above the threshold of the depression, all the water above the threshold is also contributing to outflow of the HDS model of the subbasin. In this case the contributing area fraction will be one for the next timestep, otherwise the contributing fraction is calculated with a hysteretic function. The hysteretic function will keep the contributing fraction constant if the water volume in the depression is un-changed, if it is decreasing (drying up) the contributing fraction is set to zero. If the depression is filling up, the contributing fraction is increasing linearly on a curve to reach a contributing fraction of one at the same time as the depression is filled to the max.
Input are the maximum depth (hds_depth) and maximum area (ilake slc-area) of depression in GeoData.txt (or a ilakeregion dependent parameter hdsdepth can be used). In addition, the land area fraction connected to the ilake, icatch, is used. It is set equal to one if the whole subbasin may contribute to the HDS outflow. icatch can be lower if part of the land area of the subbasin is always contributing to subbasin outflow, e.g. if it is contributing to a main river through the subbasin. The output 'connectivity' of the HDS model is in the HYPE implementation defined as the contributing area fraction, aka one minus the non-contributing area fraction. This because, at the moment, the water area of the depression is constant. The output 'non-contributing area fraction' is a the fraction of the ilake catchment area (including the ilake area itself) not contributing to outflow from the HDS model.
The outlet lake receives both local runoff and inflow from upstream areas via the main river. An outlet lake may receive inflow from regional groundwater flow (Figure 7).
If the water level (wlm) is higher than the threshold (lake_depth) the outflow is calculated with the following equation:
gratk, gratp and grata are general parameters that apply to all lakes in the model application. ratcorr is parameter region dependent model parameter for adjusting gratk to different regions. The upstream area (uparea, ) is included in the equation if parameter grata is >0. If the water level is below the threshold then the outflow is zero. If the flow calculated by the equation gives a larger outflow volume during a time step than the water volume above the threshold, the outflow is limited so that the water level do not drop below the threshold. It is possible to prescribe another minimum flow (minflow) than zero. In this case the outflow is no lower than the minimum flow as long as there is water in the lake. That is the water level can drop below the threshold.
In LakeData.txt a specific rating curve may be set instead of the general parameters. This is done by setting the rate and exp larger than zero in LakeData.txt. The outflow is also in this case limited by the threshold not to cause the water level to drop below it. It is possible to prescribe another minimum flow (minflow) than zero. In this case the outflow is no lower than the minimum flow as long as there is water in the lake. That is the water level can drop below the threshold.
A simple regulation routine can be given in LakeData.txt for selected outlet lakes. There are two main versions of regulations. The first determines a (often constant) production flow, for water levels between the lake threshold and a lower water stage threshold, and a spill for higher water levels. The second determines the outflow by different rating curves for (two) different seasons. For both variants it is possible to prescribe another minimum flow (minflow) than zero. In this case the outflow is no lower than the minimum flow as long as there is water in the lake. That is the water level can drop below the threshold(s).
The regulated outflow is independent of water level (wlm (m)) between the threshold (w0=lake_depth) and a minimum water level (wmin). For this interval the production flow (qprod) is used. Production flow may depend on time of year and the water level. The minimum water stage is not really a water stage, but is calculated from the regulation volume (regvol) and the lake (surface) area. Thus it does not consider the area changing with depth.
For water levels above the threshold, the flow is calculated with a rating curve (typically flow through spillways) or all the water above the threshold is discharged. In this case though, the calculated flow may be increased so that the outflow is at least equal to the production flow (qprod). Compiled together as one equation, the outflow from a regulated lake is:
Input variables rate, exp, qprod, regvol, w0, qamp and qpha can be found in LakeData.txt. The variable wmin is calculated by the program from regvol and lake area:
Production flow can have two different values during the year, which depends on the day of the year. This is determined by the input variables qprod1, qprod2, datum1 and datum2. Regulation period 1 between datum1 and datum2 has production flow qprod1, while the rest of the year has production flow qprod2. Not setting the dates gives the same production flow the whole year (qprod1). Production flow can alternatively be made to vary sinusoidal over the years, with a peak in December, when power output is normally high, and a minimum in June. This is done with the input variable qamp. If you want a different seasonal variation set qpha (default = 102).
In addition, the production flow may be reduced when there is a low water level in the dam. The flow will then be reduced linearly from full production flow for that time of year when water level is over the limit (limqprod (percentage of volume)) to zero when no water is left in the dam over wmin level.
Regulated outflow can also be calculated from different rating curves for the regulation periods. The rating curve parameters are the specific rate and exponent for the lake, or if lacking, the general rate and exponent parameters.
Rating curve threshold (w0) determined by input variable w0ref is used for regulation period 1, while the rating curve threshold is changed for regulation period 2. The shift is determined by input variable deltaw0:
The shift between regulation period 1 and 2 can be made smoother by allowing the threshold to increase/decrease linearly over a few days. The number of days is given by the parameter w0adjdays.
In addition to regulated lakes (described above), dams in HYPE can instead be regulated by a specific purpose. Dams are then governed by the main purpose of the dam, e.g. hydropower, flood control. The rules of calculating the outflow of the dam then depends on the specified purpose of each dam. The outlet lakes that are regulated by a specified purpose is given in DamData.txt. A dam without defined purpose may use the methods given in previous sections (and be defined in LakeData.txt).
Dams are characterised by their regulation volume (regvol) between a minimum water stage (wmin) and the spill threshold (w0). The minimum water stage (wmin) is not a real a water stage, but is calculated from the regulation volume (regvol) and the dam (surface) area. Thus it does not consider the area changing with depth. Below the minimum water level no outflow occurs. The spill threshold is defined from the lake's given depth (lake_depth)
For dams a preferred production flow is calculated (see below). This is released if the dam in within the regulation volume, but no more water is released than to keep the water level above the minimum threshold. If instead the water level of the dam is above the threshold w0, the spillway equation (rating curve) is used. The outflow is the maximum of the spillway equation and the preferred production flow.
Input variables rate, exp, regvol, qamp and qpha is given in DamData.txt.
For all dams the general preferred production flow is calculated from input data on the dam. The flow that is preferred to be released from the dam today is then adjusted depending on purpose. The general production flow (qprod) may be constant or vary between two values per year. Typically it is estimated from the yearly average inflow of the dam, which is given as input data. It can alternatively be determined by input variables qprod1, qprod2, datum1 and datum2, which then has to be estimated. Regulation period 1 between datum1 and datum2 has production flow qprod1, while the rest of the year has production flow qprod2. Not setting the dates gives the same production flow the whole year (qprod1). IF qprod1 is not given qprod is estimated from the yearly average inflow of the dam, which is given as input data.
The production flow may be reduced when the water level is low in the dam. The flow will be reduced linearly from full production flow for that time of year when water level is at the limit (limqprod (percentage of volume)) to zero when no water is left in the dam over wmin level.
Dams of these purposes uses the general perferred production flow as it is.
The flood control dam will try to stay empty and ready to delay large inflows. The preferred production flow is calculated from the inflow of the day (Qinftoday) for low inflow and water stages, but set higher than the inflow for high flows and water levels. The maximum flow (qthresh, the threshold flow) is determined from input data (Qinf is average inflow to dam for each month) and a general parameter (kthr), while the water level threshold (wthres) is determined by a general parameter (klow) for the fraction of the regulation depth.
If the current inflow is larger than the threshold inflow (qthresh), the maximum allowable discharge is released:
If the current inflow is less than the threshold inflow (qthresh) and the current water level is lower than the threshold level (wthresh), the inflow is released from the dam:
If the water level is above the threshold (wthresh), more water is released than inflow in an attempt to empty the dam. The factor multiplied by inflow (krel) is a general parameter:
Dams for hydropower use the general preferred production flow, but the flow may be seasonally redistributed. The seasonal adjustment is a sinusoidal factor over the year, with as default a peak in December, when power output is normally high (in northern Europe), and a minimum in June. For a model in another geographic area, a different seasonal phase may be needed, and is then set with the input qpha to another value (default = 102).
The seasonal redistribution is used for dams/subbasins with a snowfall fraction (snowfrac) above 0.35. For these dams the seasonal variation is calculated as:
If the snow fall fraction is above 0.35, a qamp of 0.71 is used, otherwise it is zero. The size of the seasonal adjustment can alternatively be set by the input variable qamp (0<qamp<1) for each dam. To turn off the seasonal redistribution the snow fraction can be set to zero for a specific dam.
An outlet lake that is not part of a lake composed of lakebasins, may have two defined outlets in LakeData.txt. The flow of the first outlet will go to the main downstream subbasin, and the second outlet will go to the subbasin defined in BranchData.txt. The outlets is divided into different outlet types depending on method for determining the outflow. HYPE will define an outlet's type based on variables present in LakeData.txt. Below, the defining (necessary) variables are given for each outlet type. Note: The threshold (w0ref) is given for first outlet. For the second outlet this variable instead is given relative to the threshold of outlet 1 (i.e usually zero).
1. An outlet with outflow as production flow (only). The production flow can be determined by constants for different seasons or with a sinus adjustment; see Production flow above. Defining variables in LakeData.txt: regvol, (rate=0, maxQprod=0, minflow=0)
2. An outlet with outflow as production flow (same as type 1), but with an allowed (higher) maximum production flow. If the outflow from the other outlet is above zero, part of that flow will be sent through this outlet as part of production flow instead. Defining variables in LakeData.txt: regvol, maxQprod.
3. Rating curve determined outflow with constant threshold. Defining variables in LakeData.txt: rate (deltaw0=0, regvol=0, maxQprod=0)
4. Rating curve determined outflow with constant threshold relative to the threshold of the first outlet. This type is only used for the second outlet. Defining variables in LakeData.txt: rate, w0ref (regvol=0, deltaw0=0)
5. Flow determined by production flow below the threshold, and by a rating curve above the threshold. This could be production and overflow from a hydropower plant that goes too the same downstream subbasin. Defining variables in LakeData.txt: regvol, rate (maxQprod=0, minflow=0)
6. An outlet with outflow as production flow determined by different rating curves for different seasons; see Two rating curves above. Defining variables in LakeData.txt: rate, deltaw0 (regvol=0, maxQprod=0)
7. An outlet with outflow as production flow determined by two rating curves (same as type 6), but with an allowed (higher) maximum production flow. If the outflow from the other outlet is above zero, part of that flow will be sent through this outlet as part of production flow instead. Defining variables in LakeData.txt: rate, deltaw0, maxQprod (regvol=0)
8. An outlet with outflow as minimum flow. The minimum flow is determined same as production flow by constants for different seasons or with a sinus adjustment. Defining variables in LakeData.txt: regvol, minflow (rate=0, maxQprod=0)
9. Minimum flow determined by a production flow below the threshold. In addition overflow is determined by a rating curve above the threshold. This could be a minimum environmental flow together with overflow. Defining variables in LakeData.txt: regvol, rate, minflow (maxQprod=0).
10. An outlet with outflow determined from a time series in Xobs (dwtr). This type is only used for the second outlet. Defining variables in LakeData.txt: obsflow=1
Examples of common combinations of outlets:
- A hydropower plant with an estimated average production flow and a spill overflow at high water levels are simulated by combining production flow (outlet type 1) with rating curve determined overflow (outlet type 3). Note that different from a production flow and spill defined for one outlet (see Production flow above), the spill and produktion flow is here added together to form the total outflow. For one outlet the maximum of the two is used as total flow.
- Same as above a hydropower plant with production flow in one branch and overflow in another (outlet type 3), but in this case the maximum allowed production is assumed higher than the average production (outlet type 2). This means that if overflow is calculated due to high water level, part of that flow is lead to the powerplant and through production to the first branch.
- A hydropower plant where the production flow and spill goes to the same downstream subbasin (outlet type 5), but where a second spill outlet goes to another subbasin (outlet type 4).
- A hydropower plant with production flow in one branch (outlet type 1), and a minimum (environmental) flow plus overflow outlet in the old river course that goes to another subbasin (outlet type 9).
- A lake with two outlets with flow determined by a rating curve for each of them (may have different threshold also) are simulated by a combination of outlet type 3 and 4.
Many other combinations can be used, but not all outlet types are natural to combine. The following are not allowed:
| Outlet 1 | Outlet 2 |
|---|---|
| 1 | 2, 4 |
| 2 | 1, 2, 4, 7, 8, 10 |
| 3 | 5, 9 |
| 4 | all |
| 5 | 3, 9 |
| 6 | 4 |
| 7 | 2, 4, 7, 8, 10 |
| 8 | 2, 4, 7-9 |
| 9 | 3-5, 8, 9 |
| 10 | all |
After calculating the outflow from the two outlets, which is done separately, the total outflow could be higher than the volume above the threshold. In this case the outflow will be reduced. When updating the total outflow from a lake with two outlets aginst observed total flow, the flow in respective branch has to be adjusted too. Depending on the outlet types this is done by different methods.
Lakes with a clear defined division between production flow and spill branch is handled so that production flow takes priority. For outlets with a maximum production flow, flow are diverted into this branch up to the maximum value and the rest into the other branch. For other lakes with a clear defined division between production flow and spill branch, the same method is applied but with the current production flow as the maximum value. For lakes with a minimum flow in one branch the minimum flow is given highest priority. Second priority is given to the production flow of the other branch (if any). At last the remaining flow is given to the branch for spill (outlet type 9) or the non minimum flow branch (outlet type 8). For the rest of the outlet type combinations the new flows are changed to be proportional to the old flows.
An olake can be part of a larger lake. It is then called a lake basin of the larger lake, which is called a multi-basin lake. A multi-basin lake is assumed to have equal water level in all lake basins. The lake basins can have different depths below the outflow threshold, and they all use the same threshold when the water level output is calculated (same reference).
A lake basin can recieve local inflow, inflow from upstream areas (that are not part of the same multi-basin lake) and inflow from regional groundwater. Inflow works in the same way as for a simple olake (see above).
All lake basins of a multi-basin lake are connected by the main downstream path. They can in addition have branches within the multi-basin lake, where a fraction of the flow then goes. Flow through a lake divided into lake basins can occurs in both direction according to the maindown (and possibly branchdown). The implementation prioritize flow from nearby lake basins and flow in the downstream direction when calculating the flow betweeen lake basins. The flow between the lake basins are calculate to reach an equal water level. No internal threshold between lake basins is considered when the flows are calculated.
The flow out of a lakebasin (to another lakebasin) is determined in several steps:
The main outflow of the lake is assumed to be located in the last lake basin. Here outflow is estimated by a rating curve, either a specific equation or with the general equation, or by a regulation routine. The threshold may be changing over the year as described in Section Two rating curves above (below Regulated lake). If the water level is below the threshold then the outflow is zero (or other minimum flow, minflow), or if the production flow regulation is used, there is production flow. See Section Production flow above.
In addition the lake can have outflows out of the multi-basin lake from other lakebasins. These additional outflows are then the flow in the branch of these lakebasins. The outflow in a branch going out of the multi-basin lake is specified in LakeData for that lakebasin. It can be determined by a rating curve or by production flow. If it is a production flow it uses the same thresholds as those for the main outflow of the multi-basin lake, i.e. w0 and wmin.
Unless a starting state is given from a file, the lakes start the simulation filled with water to their outflow threshold. That means for most lakes a water level equal to lake_depth. Dams are filled to the dam's maximum elevation (equal to lake_depth), except for flood control dams which are initializied with an empty regulation volume.
For lakes with outflow determined by a rating curve, the water level of the lake will often be higher than the outflow threshold level. The equilibrium level will depend on the size of the inflow and the outflow rating curve parameters. Depending on the residence time of water in the lake it may take time for this level to be established, and until then the outflow of the lake will be simulated lower than it should be. Thus a spin-up time is needed for a model simulation. For lakes in arid areas and for lakes with small catchments, the water level may be below the threshold and only occasionally have outflow.
It is possible to set at date from when a dam with regulation given in LakeData or DamData is supposed to be in place and regulate the flow. The same way it is possible to give a date when the dam is supposed to be removed. For the period before the dam is build and/or after the dam is removed the outflow of the lake (that is not a dam anymore) is calculated from the rating curve parameters used for spill during regulation period.
The removal of a dam is simulated by reducing the threshold of the lake (aka reducing the lake depth) to the wmin-level. Similarly the lake depth is increased when a dam is built. The lake depth given in the input file is assumed to be the lake depth of the dam (as it is for outlet lakes without dates for building/removing the dam). The lake depth is set to the lake_depth given in input file minus the the distance calculated from regulation volume divided by lake surface area for the period without a dam. When during a simulation the date of the building or removing of the dam is passed, the lake depth used in the simulation is changed.
Removing of a filled dam may cause a flood wave travelling downstream. An option to have a smoother transition is to have an emptying phase with a gradually reducing threshold. This is implemented with a parameter specifying a number of days before the date the dam is removed that the threshold will start to decrease.
If shorter time steps are used, the dam is assumed to be build or removed on the hour 00.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| Local lake (ilake) | gldepi, illdepth, gratk, gratp, grata, ilratk, ilratp | par.txt | |
| icatch | icatch | GeoData.txt | |
| or gicatch, illicatch | par.txt | ||
| lks_num, lks_dp_N, lks_fi_N, lks_fa_N | GeoData.txt | ||
| Simple outlet lake or dam (olake) | lakedepth | lake_depth | GeoData.txt or LakeData.txt or DamData.txt |
| gldepo, olldepth | par.txt | ||
| ratcorr, olratk, olratp, kthr, klow, krel | |||
| wmin | calculated from regvol | LakeData.txt or DamData.txt | |
| rate, exp, qamp, qpha | |||
| qprod | qprod1, qprod2, datum1, datum2 | ||
| limqprod,w0adjdays | LakeData.txt or par.txt | ||
| deltaw0,minflow | LakeData.txt | ||
| purpose, snowfrac | DamData.txt | ||
| Qinf | qinfjan, qinffeb, .., qinfdec | ||
| Outlet lake with two outlets | ldtype=5 or 6 | LakeData.txt | |
| w0ref, maxQprod, minflow, obsflow | |||
| Constructing dams | builddam, removedam | LakeData.txt or DamData.txt | |
| remdamdays | par.txt |
| Modules (file) | Procedures | Sections |
|---|---|---|
| surfacewater_processes (sw_proc.f90) | calculate_potential_evaporation | evaporation |
| calculate_actual_lake_evaporation | ||
| average_flow_rating_curve | ouflow with rating curve | |
| calculate_ilake_outflow | local lake | |
| calculate_ilakesection_outflow | ||
| set_general_rating_k | simple outlet lake | |
| calculate_outflow_from_outlet_lake calculate_branched_flow | simple outlet lake | |
| outlet lake with two outlets | ||
| calculate_lake_outlet_outflow | outlet lake with two outlets | |
| calculate_lakebasin_average_waterstage | outlet lake as multi-basin lake | |
| calculate_outflow_from_lakebasin_lake | ||
| calculate_branched_flow | ||
| change_current_dam_status | constructing dams | |
| modelmodule (model_hype.f90) | initiate_model | local lake |
| calculate_local_lake_model | ||
| calculate_flow_from_undivided_lake | simple outlet lake | |
| outlet lake with two outlets | ||
| calculate_flow_for_lakebasin_lake | outlet lake as multi-basin lake |
Ahmed, M.I., Shook, K., Pietroniro, A., Stadnyk, T., Pomeroy, J.W., Pers, C., Gustafsson, D., 2023. Implementing A Parsimonious Variable Contributing Area Algorithm for the Prairie Pothole Region in the HYPE Modelling Framework. Environmental Modelling & Software. https://doi.org/10.1016/j.envsoft.2023.105769
Lindström, G., 2016. Lake water level for calibration of the S-HYPE model, Hydrology Research 47.4:672-682. https://doi.org/10.2166/nh.2016.019
Shook, K., Papalexiou, S., Pomeroy, J.W., 2021. Quantifying the effects of Prairie depressional storage complexes on drainage basin connectivity. J. Hydrol. 593, 125846. https://doi.org/10.1016/j.jhydrol.2020.125846
Floodplains may be simulated adjacent to a main river or outlet lake. Floodplain is a land area close to the surface water that may be temporary flooded. Water may flow from the surface water to the floodplain and back. The floodplain is a part (fpf) of the classarea of the main river or the lake. The lake/river surface area is the rest of the classarea. The floodplain is flooded when the water in the river or lake reaches above a certain threshold. The water on the floodplain may return to the river lake or may be trapped when the water level of the floodplain sink.
The water level of the floodplain and the extent of the flooded area (aplain, m2) are calculated from the volume (volplain, m3), maximum area (amax) and water level at maximum areal extent (fym, m). The actual water level will be compared to the equlibrium water level to determine the water exchange. The equilibrium water level is the water level we would have if water was evenly distributed in the lake and the floodplain. It is solved from a second degree equation.
The exchange of water between lake (or river) and floodplain is determined by the respective water levels (wlbody and wlplain), the equilibrium water level (wlequil) and the thresholds between the water bodies (flbody/flplain). If the water level is over the threshold and higher than the water level of the floodplain the flow from water body to floodplain is:
If the floodplain water level is over the threshold and higher than the water level of the water body the flow from floodplain to body is similarly:
Floodplain water level (wlplain) and degree of flooded area () are possible to print out from a simulation with an outlet lake or main river with floodplain.
The simple floodplain model simulates precipitation on the floodplain and evaporation from the flooded water, in addition to the exchange of water between the river or lake and the flood plain. All precipitation on the floodplain is contributing to flooded water.
The floodplain model with soil routines is calculating all soil flows for the non-flooded part of the floodplain. The runoff from the floodplain soil goes to the flooded water, and not to the local stream as it does for ordinary land classes. Precipitation and evapotranspiration is calculated for the flooded water and the non-flooded soil. For the soil part, snow, infiltration and surface runoff, percolation, tile drainage and groundwater runoff is calculated as for an ordinary soil. Infiltration from the flooded water to the soil may occur. Regional groundwater percolation is only calculated for the flooded part together with percolation from the river.
It is possible for flooded floodplains to limit the water flow from upstream rivers and lakes. This is determined based on the water levels in the floodplains, a higher water level of a downstream floodplain compared to a upstream floodplain may reduced the flow from the upstream compartment (main river or outlet lake) to the downstream compartment (main river or outlet lake). The damming flow is calculated as the flow to reach equilibrium water level between the two floodplains. The relative level of the two floodplains location is determined based om the classes average elevation and thresholds or given as indata separately. The function of connecting floodplains works within a subbasin or between connected subbasins. This floodplain features may be used together with the Floodplain model with soil routines.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| fpf | fpfol, fpfmr | FloodData.txt | |
| Common floodplain processes | classarea | slc_nn, area | GeoData.txt |
| fym | fymol, fymmr | FloodData.txt | |
| rcbodyToPlain | rclfp, rcrfp | ||
| rcplainToBody | rcfpl, rcfpr | ||
| flbody | floll, flmrr | ||
| flplain | flolp, flmrp | ||
| Connected floodplains | hrefl, hrefr |
| Modules (file) | Procedures | Sections |
|---|---|---|
| surfacewater_processes (sw_proc.f90) | add_precipitation_to_floodplain | common floodplain processes |
| calculate_floodplain_evaporation | ||
| calculate_floodplain_waterlevel | ||
| calculate_waterbody_floodplain_interflow | ||
| calculate_floodplain_volume | ||
| calculate_floodplain_equilibriumlevel | ||
| calculate_regional_floodplain_flows | connected floodplains | |
| calculate_two_floodplain_equilibriumlevel_dp | ||
| calculate_equilibrium_floodplain_level_eq1dp | ||
| calculate_equilibrium_floodplain_level_eq2dp | ||
| calculate_equilibrium_floodplain_level_eq3dp | ||
| calculate_interflow_between_floodplains2 | ||
| floodplain soilmodel (soilmodel4.f90) | soilmodel_4 | simple floodplain model |
| floodplain model with soil routines | ||
| connected floodplains |
Outflow from a subbasin may flow in one or two directions. The main flow follows the main channel, which is the downstream subbasin given by the path in GeoData.txt. If there is a bifurcation, the branch flow goes to another downstream subbasin (with subid branchid). Any of the flows may go outside the model set-ups area, they are then no longer a concern of the model.
There are three ways to determine the flow in the different channels. 1) The division of the total outflow is determined in BranchData.txt. 2) The outflow is calculated for two outlets separately and then divided into the channels. For the second alternative see Outlet lake with two outlets section above. 3) The demanded flow in the branch is prescribed (Qbranch). The prescribed flow can be constant and set in BarnchData.txt or variable and given in Xobs.txt (dwtr). If the total flow is not enough to fulfil the need, less water goes into the branch. The main channel gets the rest of the total flow.
For the first method the total outflow has been calculated the ordinary way. The flows division into the two channels is the determined by four parameters; mainpart, maxQmain, minQmain and maxQbranch, which are set in BranchData.txt. Zero values of the input data mean they are not used. The main flow (mainflow) is calculated from the totalflow (q) as:
The rest of the total flow goes in the branch. The following figures give some examples of parameter combinations.
| Symbol | Parameter/Data | File |
|---|---|---|
| branchid, Qbranch, mainpart | branchid, Qbranch, mainpart | BranchData.txt |
| maxQmain, minQmain, maxQbranch | maxQmain, minQmain, maxQbranch |
| Modules (file) | Procedures | Sections |
|---|---|---|
| surfacewater_processes (sw_proc.f90) | calculate_branched_flow | - |
| calculate_branched_flow_new | - |