Navigation
HYPE Documentation
Quick links to often-used pages:
HYPE links
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
Quick links to often-used pages:
HYPE OSC (model code)
HYPE Open data access
SMHI Hydrology Research Dep., main developer and maintainer of the HYPE model
This section explains the computations in the land routines of HYPE.
A subbasin in HYPE is divided into classes depending on land use, soil type etc. The classes are called SLC:s which stands for Soil type Land use Combination. This division can be compared to hydrological response units. Lakes and river is also classes, but this section consider only land classes.
HYPE model soil routine contains (up to) three soil layers. The number of soil layers and their respective lower limits (soillayerdepth in meters, figure 1) are listed by class in GeoClass.txt. It is possible to have a different number of layers and depth of these different classes.
The parameters of water retention in the soil are wilting point (wcwp), field capacity (wcfc) and effective porosity (wcep). These are exclusive and are specified in units of depth (figure 2). The model allocates the water retention capacity evenly between soil layers, depending on their thickness, if only one value set. It is also possible to specify one value per parameter and layer. The model uses water holding capacity in mm for the layers. These are represented in the model code and this document (figure 3) as wp(i), fc(i) and ep(i). The model parameters for the water storage capacity wcfc, wcwp, wcep (and layer depending alternative wcwp1, wcwp2, wcwp3, wcfc1, wcfc2, wcfc3, wcep1, wcep2, wcep3) depend on soil type.
The soil layer water content (mm) is represented in the document as soil(i), where i = layer, but the value also depends on the subbasin and class (figure 3). The initial value of soil water is set to wp + fc. Optionally the initial value may be set to saturation (wp + fc + ep). The upper soil layer can hold more water than the porevolume. Standing water is not treated as a separate pool.
Tile drainage can be placed in any soil layer (figure 4). The depth of the drainage pipe in meters (tiledepth) is specified in GeoClass.txt for each class. A depth of 0 m is interpreted as drainage pipes are missing.
Another depth (streamdepth) is specified in GeoClass.txt; this is the maximum depth of the drainage to stream (or ditch). Soil water below this level does not contribute to the local runoff. Note that all land runoff goes through the local river (and possibly local lake) and then the main river before it reaches the outlet lake. There is no direct runoff to lakes.
In the basic model of HYPE the land classes are calculated in parallell and have no interaction with each other. The recharge - discharge model is a modeloption to introduce a crude representation of flow of water between classes within a subbasin. Some classes are chosen to represent recharge area, and other classes represent discharge area within the subbasin. The glacier class and surface water classes cannot be included in the recharge-discharge model. Another limitation is that the model does not work with classes using rootzone leakage and travel-time soilmodels as recharge or discharge classes.
In this model a part of the (originally calculated) runoff from the recharge classes are redirected to the discharge classes where it is spread equally over their area. This means that the model is sensitive to the relative fraction of area of recharge and discharge classes in the subbasin. The water is added to the bottom soillayers of the discharge classes and can there cause upwelling of water to above soil layers. The actual runoff of the recharge classes are reduced from the originally calculated value with the part going to the discharge area. The discharge classes will have a larger runoff due to the incoming water.
The part of the runoff from a recharge class that will go the the discharge class(es) are determined by a fraction given per class, and a maximum catchment area of the discharge classes. The latter is determined by a factor (general parameter wetdisca) of the the area of the the discharge classes, a maximum ratio between recharge area and discharge area.
Some additional output variables are calculated from the soil state variables.
The groundwater level is measured negative from surface (0m) to bottom of the soil layers. A positive groundwater level means that the soil surface is below water. If the ground water table reaches above the surface, the water is calculated with 100% porosity.
The water table is found in the lowest soil layer that is not completely filled with water. Soil layers above this layer may have water in its effective porosity, but that is not included in the groundwater level output variable. The water table for a soil layer is calculated linearly from the proportion of water-filled pores of effective porosity part of the soil pore volume. If the soil moisture of a soil layer is at field capacity (or below), the groundwater level of that soil layer is at the bottom of the layer. If the pore volume is filled, the groundwater level of that soil layer is at the top of the layer.
Soil moisture deficit (smdf) is calculated for the root zone, i.e. the upper two soil layers. It is the water (in mm) needed to fill the soil (soil) to field capacity (wp+fc).
Ground frost depth (which is only calculated if the soil temperature is less than zero) depends on soil temperature (soiltemp), but also on soil water content (soil), field capacity (fc), wilting point (wp) and two parameters frost and sfrost.
There are two parameters in order to be able to choose if you want the frost depth to be land use dependent or soil dependent. The parameter for the not used dependence is set to one.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| Basic assumptions | soillayerdepth, tiledepth, streamdepth | GeoClass.txt | |
| soillayerthick | calculated from soillayerdepth | ||
| wp, fc, ep | calculated from wcwp,wcfc,wcep,wcwp1-3,wcfc1-3,wcep1-3 | par.txt | |
| Diagnostic variables | frost,sfrost | ||
| soiltemp | see needed data in Links for soil temperature | ||
| Modules (file) | Procedures | Section |
|---|---|---|
| soil_processes (soil_proc.f90) | initiate_soil_water_state | basic assumptions |
| initiate_soil_water | ||
| calculate_groundwater_table | ground water level | |
| calculate_soil_moisture_deficit | soil moisture deficit | |
| calculate_frostdepth | frost depth |
The basic simulation of snow is accumulation of snowfall to a snow pack and snow melt that releases the water to infiltration. Other processes may be included dependent on model options and parameters set. These include liquid fraction of snow simulating snow water holding capacity, evaporation and sublimation, snow heat content, refreezing of liquid water in snow.
For the simplest snow model, snow melt is calculated by temperature index. Snow melting occurs proportionally to temperature, when the temperature is greater than a threshold temperature. Other options are to considers the effect of radiation and snow cover.
The alternative snowmelt models are not fully described here yet.
The default model is a temperature index model, with or without snow cover scaling. Snow melting occurs when the temperature is greater than a threshold temperature. The potential snow that melts (pmelt) depends on the snowmelt parameter cmlt, threshold temperature parameter ttmp and air temperature (temp). Additionally snow melt may be adjusted by the snow cover (effcover). The parameter fsceff determine how large effect the snow cover scaling should have, between zero and one. The actual snow melt is limited by the amount of snow (snow in mm).
The parameters cmlt and ttmp are related to land use and cmltcorr depend on parameter region, while fsceff is general.
the second model is a temperature and radiation index model, with or without snow cover scaling. The temperature index potential snow melt is calculated the same way as the default model (pmelt). In addition potential snow melt by radiation index (rpmelt) is calculated from shortwave radiation (swrad) and albedo of the snow (albedo_snow). Additionally snow melt may be adjusted by the snow cover (effcover), see model 0.
The parameter cmrad is related to land use. Snow albedo is calculated as decreasing with the age of snow (snowage), and depend on land use specific parameters (albmax, albmin and albkexp).
The two potential melting parts are added for this model. Snow melt routine consider also that snow melt (and liquid content of snow) can refreeze for temperatures below the threshold (ttmp). The refreezing resuces the snow melt. The refreezing occur when temperature is below the threshold (ttmp) and is a fraction of the (negative) potential temperature index “snow melt”. The fraction is given by the general model parameter cmrefr.
A model option for snow heat delays the snow melt until the temperature of snow is zero. Snow temperature is calculated from snow heat and snow water equivalent. Snow heat model uses general parameters sdnsnew and snkika.
Normally snow is assumed to cover the whole class if present. Alternatively if parameters are given, snow cover fraction (fsc) within a class is calculated based on snow water equivalent (snow). The formulation is based on Samuelsson et al. (2006). During snow build up the snow cover increase as a function of snow water equivalent until a maximum value (general parameter fscmax) is reached.
It is also possible to specify a minimum snow cover (general parameter fscmin). As soon as the fractional snow cover area reaches above a certain threshold (fscmax-fsclim), the snow cover area is determined by another relation that represents the redistribution of snow during winter. In this case snow cover is dependent on maximum snow pack during the winter (snowmax) and a snow cover redistribution factor that is dependent on variation in elevation (stdelev, the standard deviation of elevation within the subbasin) and land use.
The snow distribution factor (fscdist) is determined by three land use dependent parameters; fscdist0 and fscdist1 in the linear equation and a maximum value (fscdistmax). Also in this case the snowcover is limited by the maximum and minimum value parameters. When the end of the snow season approaches (defined by general parameter fsck1) the snowmax variable is gradually decreased in order to be reset before next winter season:
The equation depends on two general parameters, fsck1 and fsckexp, where fsckexp depend on time (ts is seconds per timestep of simulation).
For winters when the snow pack does not reach the definition of large snow pack, the first equation is used during the whole season. For winters when the snow does not melt completely, the second equation is continued to be used.
There are two alternative snow depth models implemented in HYPE. Both use the snow density of fresh snow. Snow density for fresh snow is set by a general parameter (sdnsnew ~0.1). If there is wind and a wind scale parameter is given, then the fresh snow density () is scaled with the wind factor (sdnswscale and maximum snow density (sdnsmax).
In the default snow depth model, snow density (snowdens) depends on the snow's age in days (snowage). The increase of density with snow age (snowdensdt) is a general parameter (~0.002 g/cm3/d). The snow's age increases by one every time step, but are weighted with age (0) for any new snow.
In the alternative snow depth model, snow density is calculated by a compacting factor. Maximum snow density (sdnsmax), compactation rate for low temperatures (sdnsrate) and additional compactation for high temperature (sdnsradd) are all general parameters used for this model. The change in snowdensity due to snowfall is calculated from the updated snow depth (snowfall added with density ) and snow pack. The change in snowdensity (densdt) due to compactation each time step is calculated as:
for cold days (temperature is below threshold temperature parameter ttmp), and
for warm days.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| Snow | whcsnow | par.txt | |
| Snow melt | ttmp, fcseff | ttmp, fcseff | par.txt |
| cm | cmlt, cmltcorr | ||
| albmin,albmax,albkexp,cmrad | albmin,albmax,albkexp,cmrad | ||
| sdnsnew, snkika | |||
| T | calculated from | Tobs.txt | |
| Snow cover | stdelev | elev_std | GeoData.txt |
| fscmax, fscdist0, fscdist1, fsck1, fsckexp | fscmax, fscdist0, fscdist1, fsck1, fsckexp | par.txt | |
| fscmin,fsclim,fscdistmax | |||
| Snow depth | sdnsnew, snowdensdt, sdnsmax, sdnsrate, sdnsradd, ttmp, sdnswscale | par.txt | |
| wind | calculated from | Uobs.txt or UWobs.txt and VWobs.txt |
| Modules (file) | Procedures | Section |
|---|---|---|
| soil_processes (soil_proc.f90) | calculate_snow | snow melt |
| calculate_snowmelt | ||
| snowalbedo_function | ||
| calculate_snowheat_processes | ||
| snow_thermal_conductivityfunction | ||
| calculate_fractional_snowcover | snow cover | |
| calculate_snowdepth | snow depth |
Soil layer temperature (soiltemp) is calculated as a balance of three temperatures; previous time step soil layer temperature, soil temperature at deep depth (deeptemp) and air temperature (T). The model is based on Lindström et al. (2002). The weight of the deep soil is constant (0.001), while the weight of the air temperature (weightair) depends on snow depth (snowdepth) and parameters. The soil memory (soilmem) depends on depth and land use, with parameters surfmem and depthrel. The memory of deep soil temperature is a general parameter (deepmem).
Negative soil temperature will freeze part of the soil water and affect evaporation, percolation and runoff. It was used by Stadnyk et al (2020). The effect of frozen soil can be included in simulation by a model option. The model option come in two variants.
A fraction of the soil water is assumed in liquid phase for each soil layer (liqfrac). It is assumed equal in the different “pores”, i.e the same fraction frozen in water below wilting point, in water in field capacity and in water available for runoff. The fraction of liquid water for a soil layer is calculated from the temperature of the soil layer (soiltemp, degree Celsius), soil water (water), porosity (pw) and two soil type dependent parameters (parlogsatm, parbcosby):
An alternative model for calculation of liquid fraction is available. In the alternate model each soillayer is divided into three equal thick temporary layers and a soil temperature for each of these are determined. Then the fraction of liquid phase is calculated for the temporary layers based on their soil temperatures. The average of the liqfrac for the temporary layers is then applied to the soil layer in the following calculations.
Frozen soil affects evapotranspiration, percolation, soil layer runoff and tile runoff. Actual evapotranspiration is decreased by the fraction of frozen water in soil. Percolation is only acting on the liquid water of the soil. For runoff the frozen soil influences in two ways; one, the water available for runoff is reduced with the frozen fraction, and two the frozen water is assumed to expand.
The expansion of ice decreases pore volume for liquid water. In HYPE this is assumed to affect soil layer runoff by increasing the pressure level in the soil layers. Since the ice is assumed equally divided between pores, this can actually force water to fill ep-pores and have some water available for runoff even though water<wp+fc. Expansion is set with a general parameter, fzsexpand, and could be up to 10% (i.e. parameter value 0.1).
Evaporation from soil is assumed to occur from the two upper layers. The potential evaporation is assumed to decrease exponentially with depth (depending on the parameter epotdist). The potential evaporation is divided between the two layers (epotfrac) with the distribution depending on the potential evaporation in the midpoint of each soil layer (figure 6). This is then used by approximating to a rectangle. Since soil layers differ between classes, the evaporation distribution do to.
The actual evaporation from a soil layer (evap) is limited by the availability of water in the soil (soil) above the wilting point (wp, mm). Evaporation is at potential rate only if the water exceeds field capacity (fc, mm) or a (large) proportion (general parameter lp) of field capacity. In between these limits evaporation increase linearly.
The actual evaporation may also depend on soil temperature (soiltemp). It is then reduced for temperatures above land use parameter ttrig and depend on two other land use parameters (tredA, tredB) as well (Figure 3).
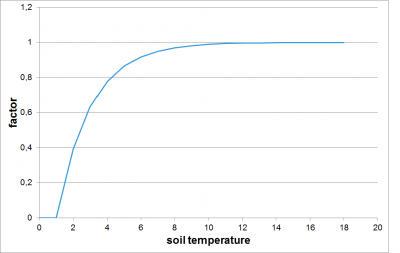 |
| Figure 8 Soil temperature factor for reduction of soil evapotranspiration. Parameter values: ttrip=1, tredA=0.5, tredB=1. |
The soil temperature evapotranspiration reduction is calculated as:
The actual soil evaporation is set to zero for temperatures below the threshold temperature and for negative potential evaporation estimates (condensation). It may also be affected by frozen soil model, which then limit evaporation to the liquid part of soil water.
Runoff depends on the water table in relation to the drainage level. Runoff occurs when soil water reaches above field capacity in the soil layers. Runoff depends on soil water in the effective porosity (also used to calculate the groundwater table) and a recession coefficient (rc). If the soil is not saturated, runoff from the soil layer depends only on the water of that soil layer. Runoff occurs from all three soil layers (runoff(k), k=1-3) down to the drainage level, which is the depth of the stream (streamdepth).
For the soillayer at drainage level, e.g. in the third layer of figure 6, and if the soil layer is not saturated, the runoff depends on the water level above the stream depth and the following equation replaces the one above.
where
If the frozen soil model is used, it influences in two ways; one, the water available for runoff is reduced to the liquid fraction, and two, the frozen water is assumed to expand possibly increasing the water level in the soil.
Soil layers that lye entirely below the stream depth have no groundwater runoff.
If a soil layer is saturated, i.e. soil>=fc+wp+ep, the runoff of the soil layer depends also on the water in the soil layer(s) above. For example if the drainage is in soil layer 3 and both soil layer 2 and 3 are saturated, the groundwater table in soil layer 1 determines the runoff of soil layer 3. The runoff is limited to the water above field capacity in the third layer though.
If the stream depth is below the bottom of the lowest soil layer. The extra distance will act as a level to increase deltah and the runoff from the lowest soillayer.
The recession coefficient is calculated from two parameters, rrcs1 and rrcs2 which depend on soil type and a parameter that is general rrcs3. The recession coefficient is assumed to decrease with depth and the parameters indicate the coefficient value in the topmost layer (rrcs1) and in the bottom layer (rrcs2). If rrcs2 is not specified it is assumed to be similar to the recession in the topmost layer. The third parameter adjusts the upper layer recession due to the subbasin gradient (slope).
The correction factor corrects rrcscorr parameters rrcs1 and rrcs2 for different parameter regions (parreg). It is defined as an increase. Note that the recession is limited to one. The recession is assumed to diminish exponentially and values of rrcs1 and rrcs2 applies to the midpoint of each layer (dk).
The variable b is an auxiliary variable.
The result is:
Runoff in the drainage pipes occurs when the water table (the percentage of filled pores of the effective porosity) rises above the pipe's depth (figure 10). Runoff depends on the groundwater surface elevation over the pipe (deltah, m), and a recession coefficient trrcs. Recession parameter trrcs depends on soil type, while drainage pipe level depends on the class. The recession parameter is adjusted with the correction parameter rrcscorr for different parameter regions (parreg). It is defined as an increase.
In addition the tile drainage can be adjusted if not the whole class is assumed to be drained by ditches. The fraction of drain area for the class is allowed to affect the recession parameter to reduce the effect of tile drainage.
where tilefrac is given per subbasin and class, or a group of classes called tilegroup.
Depending on which soil layer drainage pipe is in, the runoff will be calculated for water in that soil layer. For the soil layer k (soil(k) is the water content in soil layer k) runoff is calculated as the parameter trrcs times the water found in the effective porosity of the layer and of the overlying soil layers if it is full.
deltah = (soil(k)-wp(k)-fc(k))/ep(k) * soillayerthick(k) -
(soillayerdepth(k) - tiledepth)
IF(soil(k)-wp(k)-fc(k)-ep(k)>=0.) deltah= deltah + (soil(k-1)-wp(k-1)-
fc(k-1))/ep(k-1) * soillayerthick(k-1)
IF(deltah>0.)
runoffd = trrcs * deltah / soillayerthick(k) * ep(k)
If the frozen soil model is used, it influences in two ways; one, the water available for runoff is reduced to the liquid fraction, and two, the frozen water is assumed to expand possibly increasing the water level in the soil.
Infiltration is calculated from the sum of rain and snowmelt (infilt0, mm/time step) .
Part of the available water for infiltration (infilt0) may not infiltrate into the soil, due to limitations by the soil's infiltration capacity and other properties of the soil. The calculation of actual infiltration will consider effects of surface runoff, macropore flow and frozen soil. If the finally calculated infiltration is greater than zero, it is added to the upper layer soil water. This is done regardless of whether there is space in the soil pores there or not. If the water exceeds the water pore volume it is assumed to lie on the ground, but it still belongs to the upper soil layer, is totally mixed and thus has the same concentrations.
HYPE has an option for alternative calculation order of soil processes during a timestep. As default it calculates and add infiltration (and let the soil water percolate) before runoff and evaporation is calculated and removed from the soil water. Alternatively runoff and evapotranspiration is calculated before infiltration and percolation to slow the response of soil runoff. These options is tested during development of the soil routine.
There are alternative models for diversion of flow from water available for infiltration (infilt0) to be chosen from. All model options result in a division of available water into three flow paths; surface runoff to the nearest stream, infiltration to top soil layer, and macropore flow to the soil layer where the groundwater table is currently located.
The original and default model is based on runoff coefficients and thresholds for infiltration and soil moisture. Surface runoff due to excess infiltration and macropore flow are calculated from the sum of snow melt and rainfall; the water available for infiltration (infilt0).
If the current infiltration rate is greater than a threshold (mactrinf, mm/timestep) then macropore flow (macroflow) and surface runoff (infoverflow) may occur. In addition, the water in the upper soil layer needs to be larger than another threshold. This threshold is determined by a soil type dependent parameter (mactrsm) multiplied by the water not available for runoff (i.e. fc+wp). The two flows are calculated as a percentage (macrate respective srrate) of the infiltration above the first threshold;
All the four aforementioned parameters are soil type dependent. If macrate and srrate together are greater than one, they are weighted so that their sum is one prior to calculation of the surface runoff and macropore flow;
The actual infiltration is calculated by subtracting the macropore flow and surface runoff from the sum of snow melt and rain.
An alternative flow diversion model calculates surface runoff and macroporeflow from a surface runoff coefficient based on current (S) and maximum soil moisture (Smax). The soil moisture can be based on one, two or all three soil layers.
where soil(j) is soil water of soil layer j (mm), pw(j) is pore volume of soil layer j (mm) and calculated from the model parameters for water holding capacity (wcwp, wcfc and wcep), nlayer is set by a general model parameter (srnlayer).
The surface runoff coefficient (srratio) is a “beta-function”, with the general parameter srbeta as exponent beta
,
but limited to one. A fraction of the diverted flow goes to macropore flow (macroflow), while the rest become surface runoff (infoverflow). The infiltration (infilt) is the rest of the available water.
Another alternative flow diversion model calculates surface runoff and macroporeflow from a surface runoff coefficient based on current (S) and maximum soil moisture (Smax) and from current available water for infiltration. This model is similar to the one above but the exponent of the surface runoff coefficient (beta) is calculated from two general parameters and infilt0.
An optional model for infiltration limitation and diversion of flow considers the effect of frozen soil. It is developed based on Zhao and Gray (1999) and tried by Stadnyk et al (2020). This model redirects all or part of the remaining infiltration, after calculating the diversion of surface runoff and macropore flow as described above. Note that this is not part of the frozen soil model option described above (Soil temperature and frozen soil).
If the minimum daily temperature is less than 10 degrees and the infiltration is larger than 5mm/d an ice lens is created in the soil. In this case, and as long as the maximum daily temperature is below zero, the ice lens redirect all infiltration to surface runoff and macropore flow.
If there is no ice lens, but the soil temperature of the upper soil layer (soiltemp) is below zero the infiltration is restricted but not blocked. The infiltration is restriced by a potential infiltration adapted from Zhao and Gray (1999). The potential infiltration (potinfilt) depends on a model parameter (bfroznsoil) that is soil type dependent. It also depend on the “opportunity time” (t0), which is an estimate of the time with possible infiltration in hours;
Here soil is soil water of the upper soil layer (mm), pw is pore volume of the upper soil layer (mm) and calculated from the model parameters for water holding capacity (wcwp, wcfc and wcep), and snow is snow water equivalent (mm).
If the actual infiltration is greater than the potential infiltration then the overshoot is redirected to surface runoff and macropore flow.
The here redirected infiltration is added to the macropore flow and overland flow of the basic model proportionally to their respective model parameters (macrate and srrate).
The flow of water downward through the soil layers is only possible for water over field capacity (water in the effective porosity part of the pore volume). For a frozen soil, percolation is only acting on the liquid water of the soil. A maximum percolation (mm/d) limits the flow between soil layers. For the upper soil layer it is mperc1, and for the second soil layer it is mperc2. These parameters are soil type dependent. Flow is also limited by how much water the lower layer can receive.
Drainage from soil layer 1 to soil layer 2 is
but if there is not enough capacity in soil layer 2 the drainage is instead
and fills the second soil layer.
Drainage from soil layer 2 to soil layer 3 can be at most
for that is what the soil layer 3 can receive. If soil layer 2 does not reach field capacity with perc1x added
but if soil layer 2 with perc1x added exceeds field capacity
Regional groundwater flow is created by additional percolation from soil (see Section on Regional groundwater flow).
Flow may enter the lowest soil layer, i.e. regional groundwater flow. Upwelling to soil layers above may occur if the soil layer is filled.
Surface runoff due to a high ground water table (q, mm/time step) occurs when the water table in the upper soil layer reaches above the surface. It depends on a parameter srrcs which is dependent on land use. The recession parameter is corrected with the correction factor rrcscorr for different parameter regions (parreg). It is defined as an increase.
Runoff is removed from the uppermost soil layer. The total surface runoff (due to high ground water table and low infiltration capacity) is calculated and printed.
Macropore flow occurs when the potential infiltration and water in the upper soil layer is large (see Diversion of surface runoff and macropore flow above). It is caused by a limited infiltration capacity of the soil. Macropore flow (macroflow) is added to the layer in which the water table is located (see Diagnostic variables above). The water is added to this layer only until it is full and the excess is trapped in the layer above.
Thus water does not flow up into the layer above when macropore flow is larger than the empty space in the soil layer with the water table, as in the case of groundwater inflow. Instead the excess flow stays in the soil layer above before reaching the soil layer of the water table. This distinction is important for the substances following the macropore flow.
| Section | Symbol | Parameter/Data | File |
|---|---|---|---|
| Soil temperature and frozen soil | T | Tobs.txt | |
| deeptemp | init2 | par.txt | |
| parlogsatmp, parbcosby | logsatmp, bcosby | ||
| deepmem, surfmem, depthrel, fzsexpand | |||
| pw | pw=wp+fc+ep and calculated from wcwp, wcfc, wcep, wcwp1-3, wcfc1-3, wcep1-3 | ||
| Groundwater runoff | wp, fc, ep | calculated from wcwp, wcfc, wcep, wcwp1-3, wcfc1-3, wcep1-3 | par.txt |
| rrcs1, rrcs2, rrcs3, rrcscorr | |||
| soillayerdepth, streamdepth, tiledepth | GeoClass.txt | ||
| soillayerthick | calculated from soillayerdepth | ||
| slope | slope_mean | GeoData.txt | |
| parreg | |||
| Runoff through drainage pipes | trrcs | par.txt | |
| tilegroup | ClassData.txt | ||
| tilefrac | tilefrac_1, tilefrac_2,…,tilefrac_10 | GeoData.txt | |
| Infiltration | mactrinf, mactrsm, macrate, srrate, bfroznsoil, macfrac | par.txt | |
| pw | calculated from wc+fc+wp | ||
| beta | srbeta or calculated from sralpha, srgamma | ||
| nlayer | srnlayer | ||
| Percolation | mperc1, mperc2 | par.txt | |
| Saturated surface runoff | srrcs | par.txt |
| Modules (file) | Procedures | Section |
|---|---|---|
| soil_processes (soil_proc.f90) | calculate_soiltemp | soil temperature and frozen soil |
| calculate_weigthed_temperature | ||
| calculate_unfrozen_soil_water | ||
| calculate_three_soil_temperature | ||
| calculate_liquid_water_fraction | ||
| initiate_soil_water | groundwater runoff | |
| calculate_soil_runoff | ||
| calculate_tile_drainage | runoff thorugh drainage pipes | |
| calculate_infiltration_flow_diversion | diversion of surface runoff and macropore flow, infiltration | |
| add_infiltration | ||
| percolation | percolation | |
| add_macropore_flow | macropore flow | |
| general_water_concentration (general_wc.f90) | inflow_lowest_soillayer | upwelling |
The glacial class' area () is divided into snowfield and glacier (
). The division may vary with simulation time, but the glacier cannot be larger than the slc class' area. At simulation start the area is considered to be all glacier, unless specific information on which year the class area is valid is given. The initial glacier volume is calculated based on glacier area or set for each glacier. If the initial year is given the initial volume is valid for that date. In this case, year of the area and/or volume and the average annual change in massbalans (annmb in m/yr) is given as input data or model parameters. The initial glacier volume is then adjusted according to the difference in years (yeardiff) between simulations start and glacier area data.
The glacier volume - area relationship:
The initial glacier volume if calculated from class area:
The glacier area is correspondingly calculated from the glacier ice volume, but is limited by the class area. The relation is:
The equation coefficients coef and exp can have different values for specific glaciers. The first coefficient coef is calculated as the product of EXP( c), where c is a glacier volume correction, and a general parameter (glacvcoef/glacvcoef1) depending on glacier type. The second coefficient, exp is a general parameter (glacvexp/glacvexp1) depending on glacier type. Glacier density (glacdens) is a general model parameter (m3 water / m3 ice).
Glaciers are divided into four types. The default type is mountain glacier, the alternatives are ice cap, ice sheet and infinite glacier. Glacier type is given as input, or determined by the glacier area (a threshold (glac2arlim, a general parameter). The glacier area is used to determine the glacier type if it is not given as input and the threshold parameter is set. The glaciers will then be divided into mountain glaciers and ice caps.
The default glacier and the ice cap glacier type differ by having different parameter values for the volume-area relationship. The default values for the volume-area relationship are based on Radic and Hock (2010).
The ice sheet glacier do not simulate an snow field, and the glacier will have a constant area. The ice sheet glacier type is thus not depending on the volume-area relationship, except for initial volume if that is not given. In that case the initial volume of the ice sheet glacier will used the ice cap parameter values.
The infinite glacier type is independent on glacier volume, because the glacier melting is not limited by the glacier volume. It has a constant area (the class area) and do not simulate an snow field.
For snowfields, all soil processes are calculated as for the common land classes. Snow pack is only calculated for the snowfield, i.e. snow depth is assumed zero on glaciers. For glaciers, all precipitation is added to the glacier ice. Glacier melting is calculated as:
where cmlt is the general parameter glaccmlt and ttmp the general parameter glacttmp.
An alternative glacier melting model exist, which depend on class' temperature (T) and radiation (swrad) and has a refreezing component (goverened by general parameter crefr). The radiation component depend on the albedo of the glacier, which in turn depends on if the glacier is snow covered (snowcov) or not, and general parameters for rate (cmrad) and glacier ice albedo (glacalb). The refreezing component is limited to the glacier melt.
Glacier evaporation is optional and set by an model option (snowevaporation). The evaporation is determined as a fraction of the potential evaporation by the general model parameter fepotglac.
Glacier melting, snow melting on snowfield and/or rain are added to the soil. Thus the soil represents the whole glacier class area. The concentrations in the glacial melt water are zero. This means that any atmospheric deposition of nutrients is lost on the glacier.
The soil water is calculated as described above.
| Symbol | Parameter/Data | File |
|---|---|---|
| classarea | slc_nn, area | GeoData.txt |
| annmb | annualmb | GlacierData.txt |
| or glacannmb | par.txt | |
| yeardiff | calculated from slcdate | GlacierData.txt or par.txt |
| and bdate | info.txt | |
| c | logvolcorr | GlacierData.txt |
| glactype | ||
| T | see needed data in Links for temperature | |
| swrad | calculated or from | SWobs.txt |
| coef | glacvcoef or glacvcoef1 | par.txt |
| exp | glacvexp or glacvexp1 | |
| cmlt, ttmp | glaccmlt, glacttmp | |
| albedosnow | calculated from snalbmin, snalbmax, snalbkexp | |
| glacalb, glacdens, glac2arlim,fepotglac | ||
| crefr, cmrad | glaccrefr, glaccmrad |
| Modules (file) | Procedures |
|---|---|
| glacier_soilmodel (glacier_soilmodel.f90) | soilmodel_3 |
| initiate_glacier | |
| initiate_glacier_state | |
| calculate_glacier_area | |
| get_glacier_parameters |
Lindström, G., K. Bishop, and M. Ottosson Löfvenius, 2002. Soil frost and runoff at Svartberget, northern Sweden - measurements and model analysis, Hydrological Processes, 16:3379-3392.
Radic, V. and Hock, R., 2010. Regional and global volumes of glaciers derived from statistical upscaling of glacier inventory data, J. Geophys. Res., 115, F01010, doi:10.1029/2009JF001373.
Samuelsson, P., S. Gollvik, and A. Ullerstig, 2006. The land-surface scheme of the Rossby Centre regional atmospheric climate model (RCA3), SMHI Report Meteorologi Nr 122, 25 pp.
Stadnyk, TA, MK MacDonald, A Tefs, SJ Déry, K Koenig, D Gustafsson, K Isberg, and B Arheimer. 2020. Hydrological modeling of freshwater discharge into Hudson Bay using HYPE. Elem Sci Anth, 8: 43. doi:10.1525/elementa.439
Zhao, L., and D.M. Gray 1999. Estimating snowmelt infiltration into frozen soils, Hydrological Processes, 13:1827-1842.